切线长定理.7-切线长定理-演示文稿-(2)VIP免费

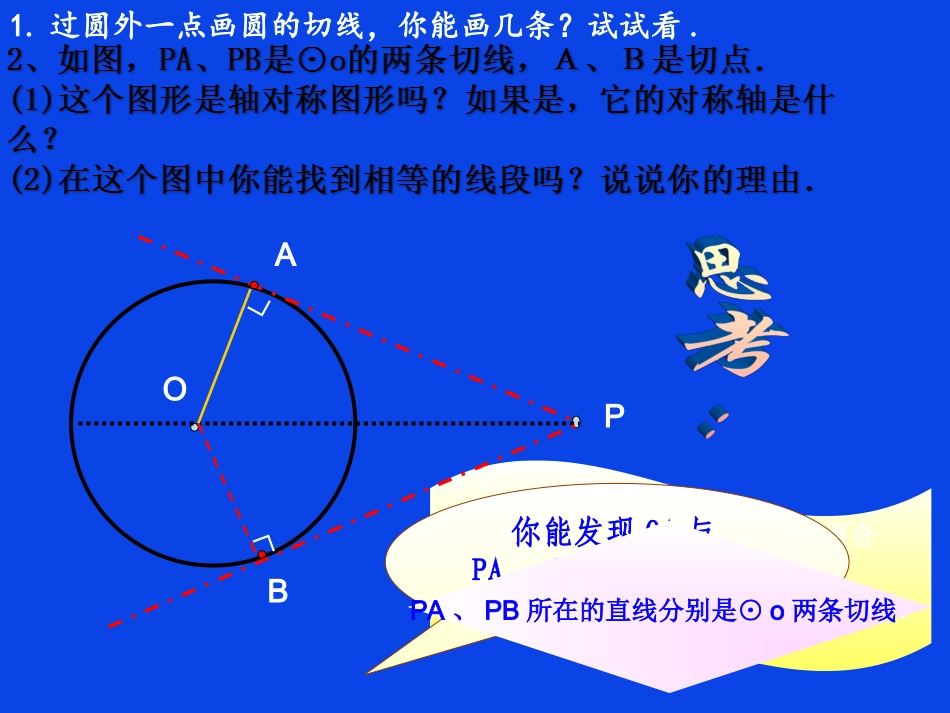
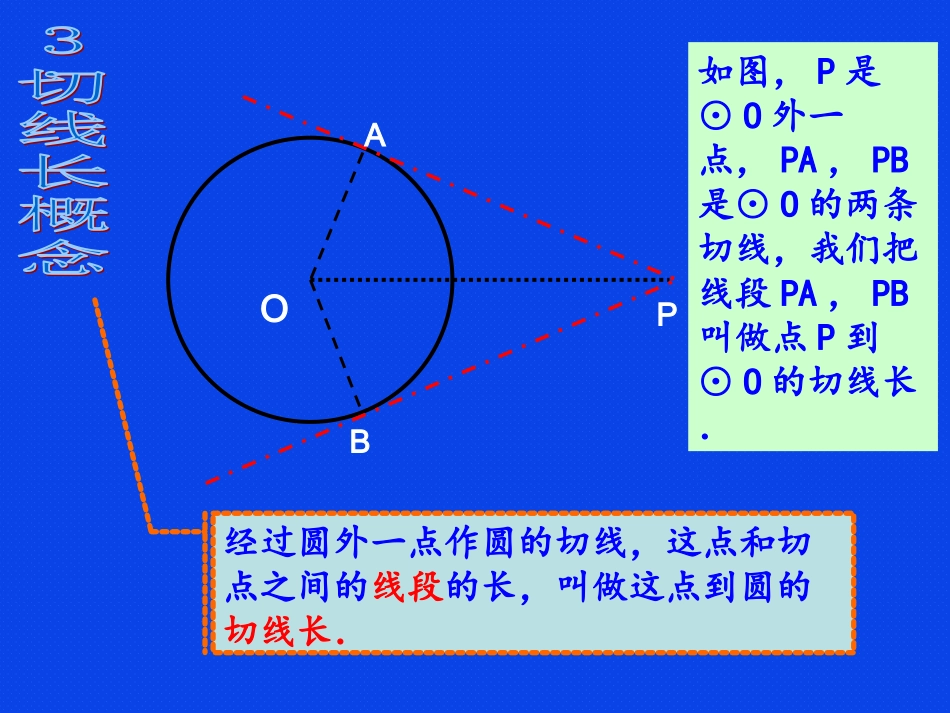
切线长定理根据圆的轴对称性，存在与A点重合的一点B，且落在圆上，连接OB，则它也是⊙o的一条半径。OPAB你能发现OA与PA，OB与PB之间的关系吗？PA、PB所在的直线分别是⊙o两条切线．∟∟1.过圆外一点画圆的切线，你能画几条？试试看.经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长．如图，P是⊙O外一点，PA，PB是⊙O的两条切线，我们把线段PA，PB叫做点P到⊙O的切线长．OPAB切线和切线长是两个不同的概念，切线是直线，不能度量；切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量。OPAB切线和切线长的区别A根据你的直观判断，猜想图中PA是否等于PB？∠1与∠2又有什么关系？证明：∵PA、PB是⊙o的两条切线，∴OA⊥AP，OB⊥BP，又OA=OB，OP=OP，∴RtAOPRtBOP△≌△（HL）∴PA=PB，∠1=2∠OPB∟∟M⌒⌒12过圆外一点所画圆的两条切线长相等，这一点和圆心的连线平分两条切线的夹角．OPB∟∟M⌒⌒12A切线长定理：∵PA、PB分别是⊙O的切线，点A、B分别为切点，（PA、PB分别与⊙O相切于点A、B）∴PA=PB，∠APO=∠BPO.4、剖析定理：（1）指出定理的题设和结论；（2）用符号语言表示定理：ABPO图3例题1：已知如图，Rt△ABC的两条直角边AC=10，BC=24，⊙O是△ABC的内切圆，切点分别为D,E,F，求⊙O的半径。例题1图AFBDEOC解：连结OD,OE,OF,则OD=OE=OF，设OD=r.在Rt∆ABC中，AC=10,BC=24∴AB=2624102222BCAC∵⊙O分别与AB,BC,AC相切于点D,E,F,∴ODAB,OEBC,OFAC,BD=BE,AD=AF,CE=CF.⊥⊥⊥又∵∠Ｃ＝90°∴四边形OECF为正方形．∴CE=CF=r∴BE=24-r,AF=10-r.∴AB=BD+AD=BE+AF=24-r+10-r=34-2r∵AB=26∴26=34-2r∴r=4,即⊙Ｏ的半径为4.请同学们想一想，这道题还有其它解法吗？•习题1：如图，P是⊙O外一点，PA与PB分别⊙O切于A、B两点，DE也是⊙O的切线，切点为C，PA=PB=5cm，求△PDE的周长.OABDCEP•习题2：如图，△ABC的内切圆⊙O与BC，CA,AB分别相切于点D，E，F，且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.第2题OFEDCBA应用新知，体验成功1、填空：如图10，PA、PB分别与⊙O相切于点A、B，（1）若PB=12，PO=13，则AO＝＿（2）若PO=10，AO=6，则PB=；（3）若PA=4，AO=3，则PO=；PD=；D图10OPBA５８５２2、已知如图10，PA、PB分别与⊙O相切于点A、B，PO与⊙O相交于点D，且PA=4cm,PD=2cm.求半径OA的长.D图10OPBA梳理小结，盘点收获1、你的学习心得、体会是什么？2、你有哪些好的经验可推广？3、你还存在哪些困难、疑问？