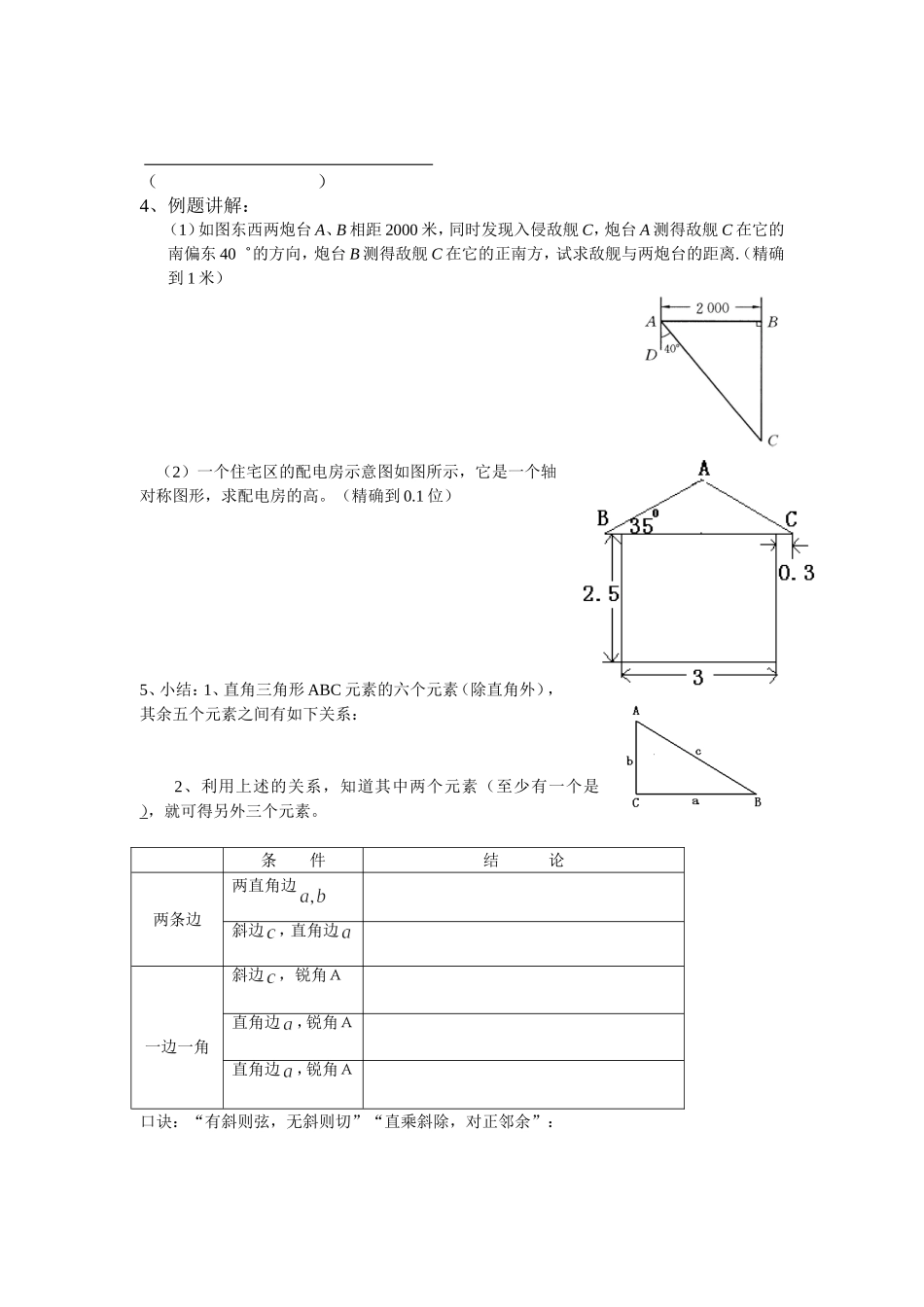
解直角三角形一、学习目标:1、理解直角三角形中五个元素的关系。2、经历运用锐角三角函数、勾股定理等知识解决直角三角形中,由已知的一些边角、求出另一些边角的过程,了解解直角三角形的概念。3、会运用锐角三角函数、勾股定理等知识解直角三角形。以及会解与直角三角形有关的简单实际问题。二、学习过程:1、试一试:如图所示,一棵大树在一次强烈的地震中于离地面3米处折断倒下,树顶落在离树根5米处.大树在折断之前高多少?在上题中,我们还可以利用直角三角形的边角之间的关系能否求出另外两个锐角?.问:若大树的折断处不易测量,只量得树顶离树根5米及树尖与水平面的的夹角30度。能否计算大树在折断之前高多少2、像这样,在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫解直角三角形。在直角三角形ABC中,,分别是的对边,问:各元素之间有什么关系?(1)两锐角的关系:(2)三边的关系:(3)边角的关系:3、你能否编写一道“直角三角形的问题,让你的同学来验证一下是否能求得其它元素?规纳:解直角三角形,已知元素(除直角外)有下面情况:()4、例题讲解:(1)如图东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)(2)一个住宅区的配电房示意图如图所示,它是一个轴对称图形,求配电房的高。(精确到0.1位)5、小结:1、直角三角形ABC元素的六个元素(除直角外),其余五个元素之间有如下关系:2、利用上述的关系,知道其中两个元素(至少有一个是),就可得另外三个元素。条件结论两条边两直角边斜边,直角边一边一角斜边,锐角A直角边,锐角A直角边,锐角A口诀:“有斜则弦,无斜则切”“直乘斜除,对正邻余”: