19.1.1矩形的性质VIP免费

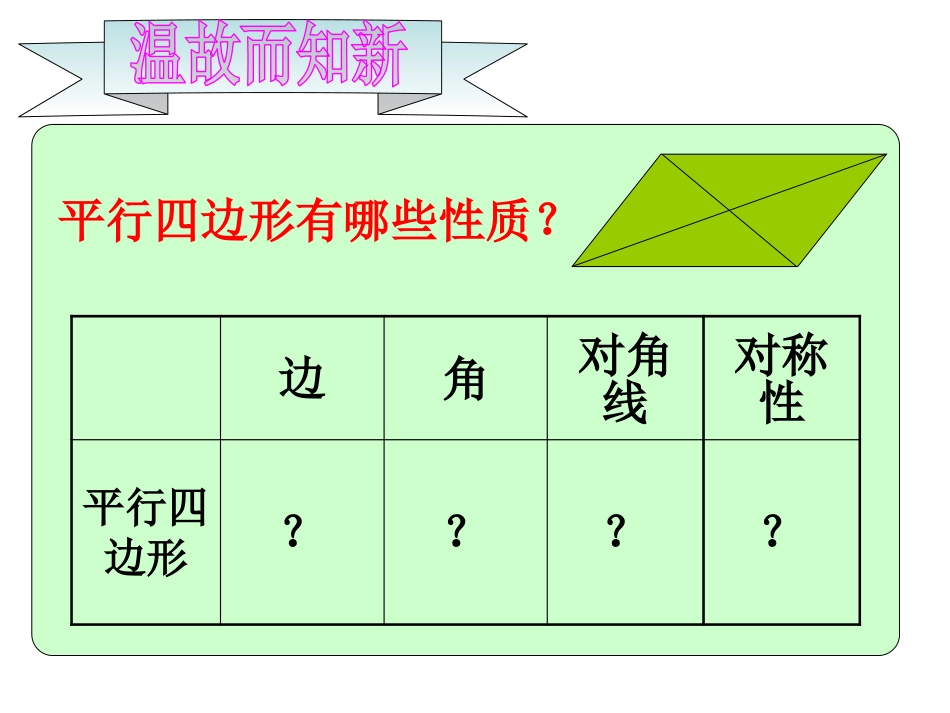
19.1.1矩形的性质19.1.1矩形的性质平行四边形有哪些性质？边角对角线对称性平行四边形？？？？平行四边形有哪些性质？边角对角线对称性平行四边形中心对称图形对边平行且相等对角相等邻角互补对角线互相平分我们已经知道平行四边形是特殊的四边形，因此平行四边形除具有四边形的性质外，还有它的特殊性质，同样对于平行四边形来说也有特殊情况，这堂课我们就来研究一种特殊的平行四边形——（课题---------）用四段木条做一个ABCD的活动木框，将其直立在桌面上并轻轻地推动，你会发现什么?试一试DACBDACBOO┓90°平行四边形矩形一个角是直角有一个角是直角的平行四边形叫做矩形。矩形平行四边形❶拿出一张矩形形状的纸张，沿不同方向对折一下，观察折痕两侧的图形，你发现什么？矩形是一个特殊的平行四边形，除了具有平行四边形的所有性质外，还有特殊性质。下面我们共同研究矩形的特殊性质，请大家做一做：OABCD矩形是轴对称图形，对称轴是经过对边中点的直线(有2条）。❷请同学们用量角器度量你的课本每个角的度数,用直尺度量两条对角线的长度.并且根据你得到的数据提出你的猜想．要大胆,不要拘束.做一做：猜想1：矩形的四个角都是直角．猜想2：矩形的对角线相等．ABCD矩形的四个角都是直角已知：四边形ABCD是矩形,B=90°∠求证：∠A=B=C∠∠=D=90°∠DCBA命题1：1:矩形的四个角都是直角DCBA证明： 四边形ABCD是平行四边形，∠B=90°∴∠B=D=90°∠又 ∠B+C=180∠°∴∠C=∠A=90°∴∠A=B=C=D=90∠∠∠°.命题矩形的性质定理1：矩形的四个角都是直角。已知：四边形ABCD是矩形，求证：AC=BD.ABCD矩形的对角线相等．命题2ABCD证明： 矩形ABCD.∴∠ABC=DCB=90°∠又 AB=DC，BC=CB∴△ABCDCB≌△∴AC=BD矩形的对角线相等．命题2矩形的性质定理2：矩形的对角线相等。边角对角线对称性平行四边形矩形O这是矩形所特有的性质ABCD边角对角线对称性平行四边形矩形对边平行且相等对角相等邻角互补对角线互相平分中心对称图形对边平行且相等四个角都是直角对角线互相平分且相等中心对称图形轴对称图形O这是矩形所特有的性质ABCD∴AD=BC，CD=AB∴ADBC∥，CDAB∥∴AC=BDABCDO∴AO=CO，OD=OB 四边形ABCD是矩形 四边形ABCD是矩形 四边形ABCD是矩形 四边形ABCD是矩形∴∠ABC=BCD=CDA∠∠=DAB∠=90︒矩形的性质数学语言 四边形ABCD是矩形❶对边平行❷对边相等❸四个角都是直角❹对角线相等❺对角线互相平分例1：如图，矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形的周长的和是86cm,对角线长是13cm，那么矩形的周长是多少？ＯABDC △AOB、△BOC、△COD和△AOD四个三角形的周长和为86cm，又 AC=BD=13cm（矩形的对角线相等）∴AB+BC+CD+DA＝86－2(AC+BD)＝86－2×2×13答：矩形ABCD的周长等于34cm。例1：解：ＯABDC＝34(cm)即AB+BC+CD+DA+2(AC+BD)＝86cm四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处，目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么？OABCDABCD公平,因为OA=OC=OB=OD四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处，目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么？OABCDABCD答案：及时练习：1、（课本P100练习）第1题：如图，在矩形ABCD中，对角线AC与BD相交于点O，试找出图中相等的线段与相等的角。ＯABDC1、（课本P100练习）第1题解：相等的线段有：AB=CD,BC=AD,BD=AC,OA=OC=OB=OD,相等的角有：∠ABC=BCD=CDA=DAB∠∠∠=90︒，∠OBA=OAB=ODC=OCD,∠∠∠∠OAD=ODA=OBC=OCB,∠∠∠∠BOC=AOD,∠∠AOB=COD.∠ＯABDC2.(课本P100第2题)如图，矩形ABCD的两条对角线交于点O，且∠AOD＝120°.求证：AC＝2AB.ＯABDC2.证明： 四边形ABCD是矩形，∴OA=OC=OB=OD, ∠AOD=120°，∴∠AOB=60°∴△AOB是等边三角形，∴AB=OA=OB,∴AC=2AB.ＯABDC练一练3.(课本P100第3题)如图，在矩形ABCD中，点E在边CD上，将该矩行沿着AE折叠，恰好使点D落在边BC上的点F处,如果∠BAF＝60°，求∠DAE的大小。练一练3.解： 四边形ABCD是矩形，∴∠BAD=90° ∠BAF=60°∴∠FAD=90°-60°=30°.根据图形折叠的性质，得∠DAE=FAE∠=×30°=15...