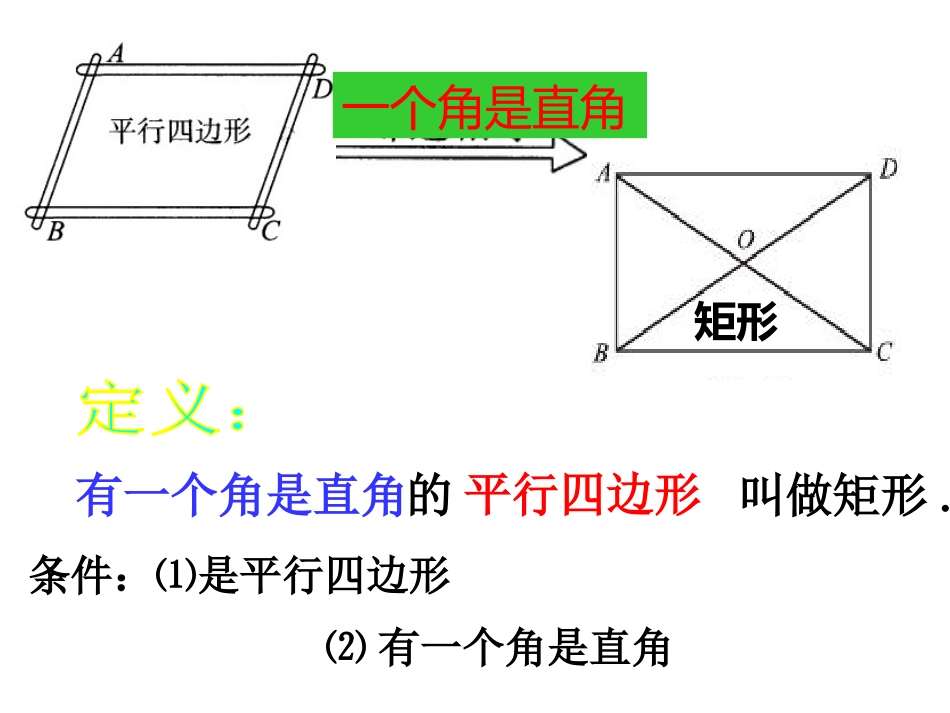
第一章特殊平行四边形§1.2矩形的性质与判定(第1课时)观察思考有一组邻边相等的平行四边形叫做矩形.条件:⑴是平行四边形⑵有一个角是直角平行四边形有一个角是直角一个角是直角矩形探索归纳矩形的一般性质中心对称图形两组对边平行且相等对角相等两对角线互相平分想一想(课本P11)1)矩形是特殊的平行四边形,它具有一般平行四边形的所有性质,你能列举出这些性质吗?2)准备好一个矩形,利用这个矩形来探索矩形还有哪些特殊的性质?与同伴交流。结论汇总:矩形的性质中心对称图形、轴对称图形(2条对称轴)两组对边平行且相等四个角相等,都是直角两对角线相等且互相平分对称性边角对角线初试证明命题:矩形的四个角都是直角,矩形的对角线相等已知:如图,四边形ABCD是矩形,∠ABC=90°对角线AC与DB相交于点O。求证(1)∠ABC=∠BCD=∠CDA=∠DAB=90°(2)AC=BD矩形的性质定理中心对称图形、轴对称图形(2条对称轴)两组对边平行且相等四个角相等,都是直角两对角线相等且互相平分巩固训练1.矩形具有而平行四边形不具有的性质是()A.对边互相平行B.对角线互相平分C.对角相等D.对角线相等D巩固训练2.如图,在矩形ABCD中,对角线AC与BD相交于点O,下列说法错误的是()A.∠ABC=90°B.AC=BDC.OA=OBD.OA=ADDOADCB归纳升华议一议(课本P12):如图,矩形ABCD的对角线AC与BD交于点E,那么BE是RtABC△中一条怎样的特殊线段?它与AC有什么大小关系?由此你能得到怎样的结论?EABC定理:直角三角形斜边上的中线等于斜边的一半.推理格式:∵∠ABC=90°,BD为斜边AC上的中线∴BD=AD=CD=1/2AC巩固训练1)已知△ABC中,∠ABC=90°,BD是斜边AC上的中线.(1)若BD=3㎝,则AC=_____㎝;(2)若∠C=30°,AB=5㎝,则AC=_____㎝,BD=_____㎝.巩固训练2)如图,在Rt△ABC,∠ACB=90°,点D、E、F分别为AB、AC、BC的中点,若CD=3㎝,则EF=_____㎝.EDFACB自学例题例1:如图,在矩形ABCD中,两条对角线相交于点O,∠AOD=120°,AB=2.5cm,求矩形对角线的长。课堂练习:1)随堂练习2)习题1.4第1题巩固训练课堂作业:习题1.4第2、3题