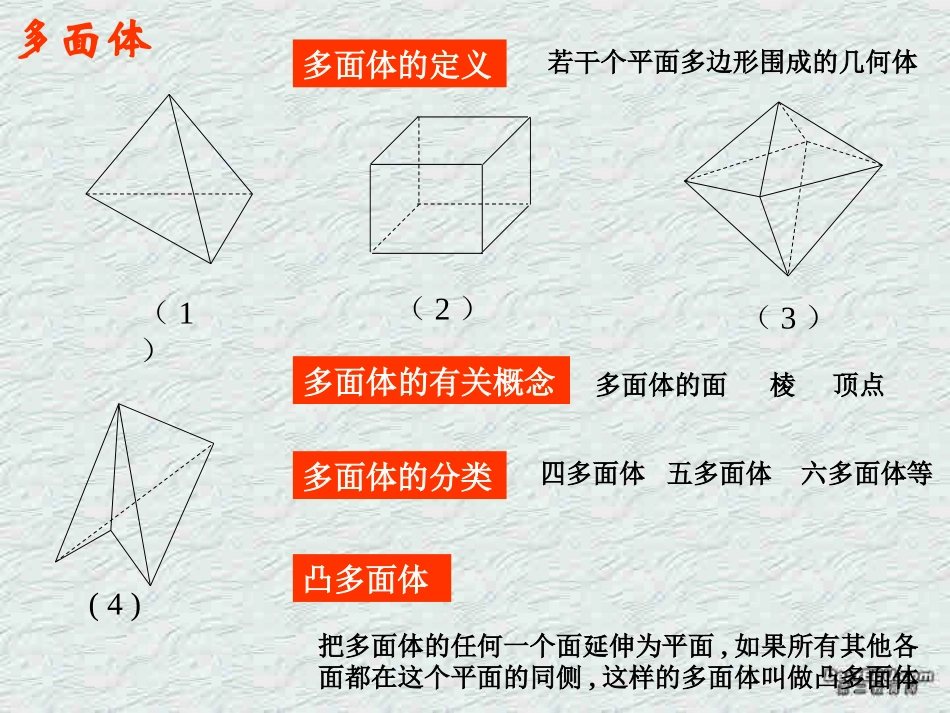
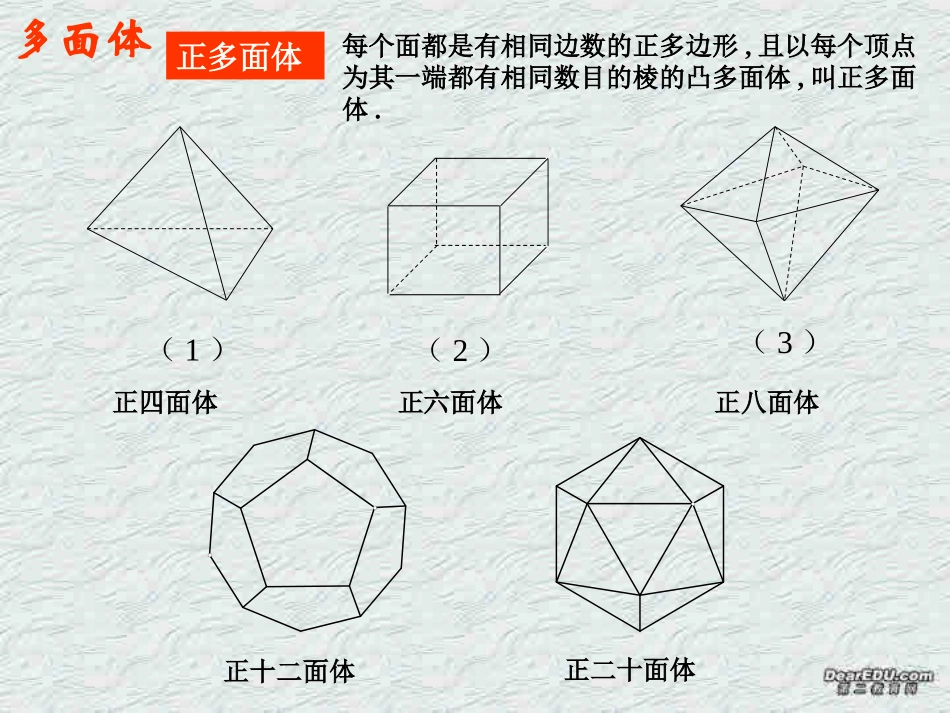
欧拉欧拉公式著名的数学家,瑞士人,大部分时间在俄国和法国度过.他16岁获得硕士学位,早年在数学天才贝努里赏识下开始学习数学,毕业后研究数学,是数学史上最高产的作家.在世发表论文700多篇,去世后还留下100多篇待发表.其论著几乎涉及所有数学分支.他首先使用f(x)表示函数,首先用∑表示连加,首先用i表示虚数单位.在立体几何中多面体研究中,首先发现并证明欧拉公式.多面体多面体的定义若干个平面多边形围成的几何体(1)(2)(3)(4)多面体的有关概念多面体的面棱顶点凸多面体把多面体的任何一个面延伸为平面,如果所有其他各面都在这个平面的同侧,这样的多面体叫做凸多面体多面体的分类四多面体五多面体六多面体等多面体正多面体每个面都是有相同边数的正多边形,且以每个顶点为其一端都有相同数目的棱的凸多面体,叫正多面体.(1)(2)(3)正四面体正六面体正八面体正十二面体正二十面体每个面都是有相同边数的正多边形,且以每个顶点为其一端都有相同数目的棱的凸多面体,叫做正多面体。正四面体及其展开图正八面体及其展开图正二十面体及其展开图正十二面体及其展开图正六面体及其展开图正多面体:多面体(6)(7)(8)简单多面体表面经过连续变形能变成一个球面的多面体(5)讨论问题1:(1)数出下列四个多面体的顶点数V、面数F、棱数E并填表(1)(2)(3)(4)图形编号顶点数V面数F棱数E(1)(2)(3)(4)规律:V+F-E=2464861268129815(欧拉公式)(7)(8)(5)5851212247812问题1:(2)数出下列四个多面体的顶点数V、面数F、棱数E并填表图形编号顶点数V面数F棱数E(5)(7)(6)V+F-E=2(欧拉公式)简单多面体讨论以上发现让我们体会了数学家欧拉的发现过程,问题1.但这并没有证明,不过让我们先记住这个结论吧,并用它来解决一些问题.先用三棱柱、四棱锥来验证欧拉公式是否正确?都满足欧拉公式.问题2.一个简单多面体的各个面都是三角形,证明它的顶点数V和面数F有F=2V-4的关系.分析:每个面都是三角形,有三条边,则F个面共有3F条边,又每条边是两相邻面的公共边,即每两条边合为一条棱,所以E=23F,代入即得.例1、简单多面体的每个面都是五边形,且每个顶点的一端都有三条棱,求这个多面体的面数和棱数及顶点数.分析:关健是寻找V,F.E关系.事实上:设面数为F,顶点数为V,棱数为E,因为每个面都是五边形,所以共有5F条边,而每两条边合成一条棱,共有25F条棱,所以有E=25F另一方面:每一顶点处有三条边,共有3V条边,每两条边合成一条棱,所以E=3532,23FEVV所以代入可求V=20,F=12,E=30.定义:正多面体的每个面是全等的多边形,每个顶点出发有相同数目的棱.设正多面体有F个面,每个面都是n边形,每一个顶点出发有m条棱.其中m≥3,n≥3。那么:,22nFmVEE得到:22,EEFVnm代入欧拉公式得到:2211112,:2EEEmnEmn即因此:m和n不可能都大于3,必定有一个等于3!为什么?推导正多面体的种类.小结:简单多面体V,F,E之间关系为:(1)E=V+F-2(2)E=各面多边形边数之和的一半(3)E=顶点数V与共顶点的棱数之积的一半问题3:欧拉公式的应用例21996年的诺贝尔化学奖授予对发现C60有重大贡献的三位科学家.C60是有60个C原子组成的分子,它结构为简单多面体形状.这个多面体有60个顶点,从每个顶点都引出3条棱,各面的形状分别为五边形或六边形两种.计算C60分子中形状为五边形和六边形的面各有多少?解:设C60分子中形状为五边形和六边形的面各有x个和y个.由题意有顶点数V=60,面数=x+y,棱数E=(3×60)21根据欧拉公式,可得60+(x+y)-(3×60)=221另一方面,棱数也可由多边形的边数来表示,即(5x+6y)=(3×60)2121由以上两个方程可解出x=12,y=20答:C60分子中形状为五边形和六边形的面各有12个和20个.例3、有没有棱数是7的简单多面体?解:假设有一个简单多面体的棱数E=7.根据欧拉公式得V+F=E+2=9因为多面体的顶点数V≥4,面数F≥4,所以只有两种情形:V=4,F=5或V=5,F=4.但是,有4个顶点的多面体只有4个面,而四面体也只有四个顶点.所以假设不成立,没有棱数是7的简单多面体问题3:欧拉公式的应用1、(1)一个简单多面体的各面都是三角形,证明它的顶点数V和面数F有F=2V-4的关系.练...