系数性质 高二数学排列组合二项式定理概率课件集三 人教版 高二数学排列组合二项式定理概率课件集三 人教版VIP免费

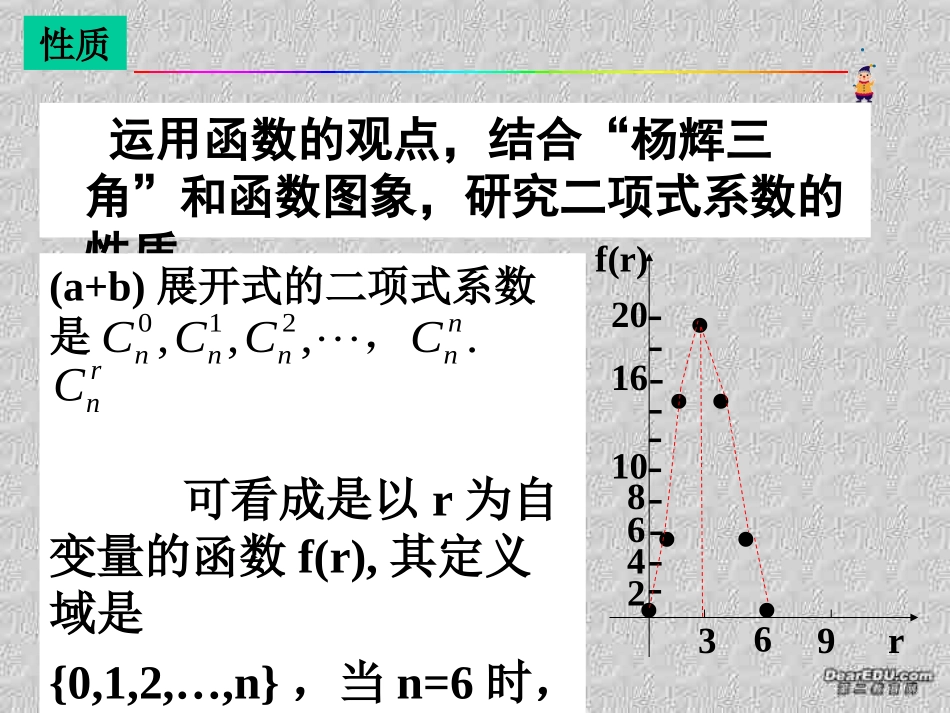
二项式定理二项式定理(2)(2)二项式定理二项式定理(2)(2)二项式定理二项式定理(2)(2)二项式定理二项式定理(2)(2)引入(a+b)1………………11(a+b)2………………121(a+b)3……………1331(a+b)4…………14641(a+b)5………15101051(a+b)6……1615201561观察二项式系数表，寻求其规律：31015性质运用函数的观点，结合“杨辉三角”和函数图象，研究二项式系数的性质．(a+b)展开式的二项式系数是可看成是以r为自变量的函数f(r),其定义域是{0,1,2,…,n}，当n=6时，其图象是右图中的7个孤立点..,,,210nnnnnCCCC，rnC..----------1084621620f(r).....369r性质（1）对称性.与首末两端“等距离”的两个二项式系数相等．..----------1084621620f(r).....369r例如：154626CC.mnnmnCC理由：2nr结论：直线将图象分成对称的两部分，它是图象的对称轴。性质（2）增减性与最大值...----------1084621620f(r).....369r增减性的实质是比较的大小。1knknCC与.11kknCCknkn作商：.2111nkkkn由21nk结论：当，二项式系数递增。由对称性知当递减。且在中间取得最大值。21nk性质当n是偶数时，(a+b)n展开式中间的一项（第项）二项式系数取得最大值；当n是奇数时，(a+b)n展开式中间的两项（第项）二项式系数取得最大值。2nnC12n121,121nn2121,nnnnCC(a+b)5………15101051(a+b)6……1615201561（3）各二项式系数的和.即求.210nnrnnnnCCCCC性质在公式令x=1，则nnnrrnnnnnxCxCxCxCCx2210)1(.2210nnnrnnnnCCCCC启示：在二项式定理中，对a,b赋予一些特定的值，是解决二项式有关问题的一种重要方法——赋值法。性质应用例1证明在(a+b)n的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和。结论131202nnnnnCCCC答案:1(1)a+b(2)126(3)210(4).21巩固练习1、二项式(1-x)4n+1的展开式中，二项式系数最大的项是第项，系数最大的项是第项。2、设含有10个元素的集合的全部子集数为S，其中由3个元素组成的子集数为T，则T/S的值为。3、已知(1-2x)7=a0+a1x+a2x2+…+a7x7，则a1+a2+…+a7的值是.提高练习1、求证:.)()()()(22222120nnnnnnnCCCCC略证：由(1+x)n(1+x)n=(1+x)2n，两边展开后比较xn的系数得：再由得nnnnnnnnnnnnnnnnnCCCCCCCCCCC201122110mnnmnCC.)()()()(22222120nnnnnnnCCCCC提高练习2、在(3x-2y)20的展开式中，求：（1）二项式系数最大的项。（2）系数绝对值最大的项。（3）系数最大的项。解:(2)设系数绝对值最大的项是第r+1项。则1211202020119120202023232323rrrrrrrrrrrrCCCC提高练习（3）因为系数为正的项为奇数项，故可设第2r-1项系数最大。（以下同2）r=5.即3(r+1)>2(20-r)得2(21-r)>3r所以当r=8时，系数绝对值最大的项为528527r812812820923yxCT小结1、当n10时常用杨辉三角处理二项式系数问题。2、利用杨辉三角和函数图象可得二项式系数的对称性、增减性和最大值。3、常用赋值法解决二项式系数问题。