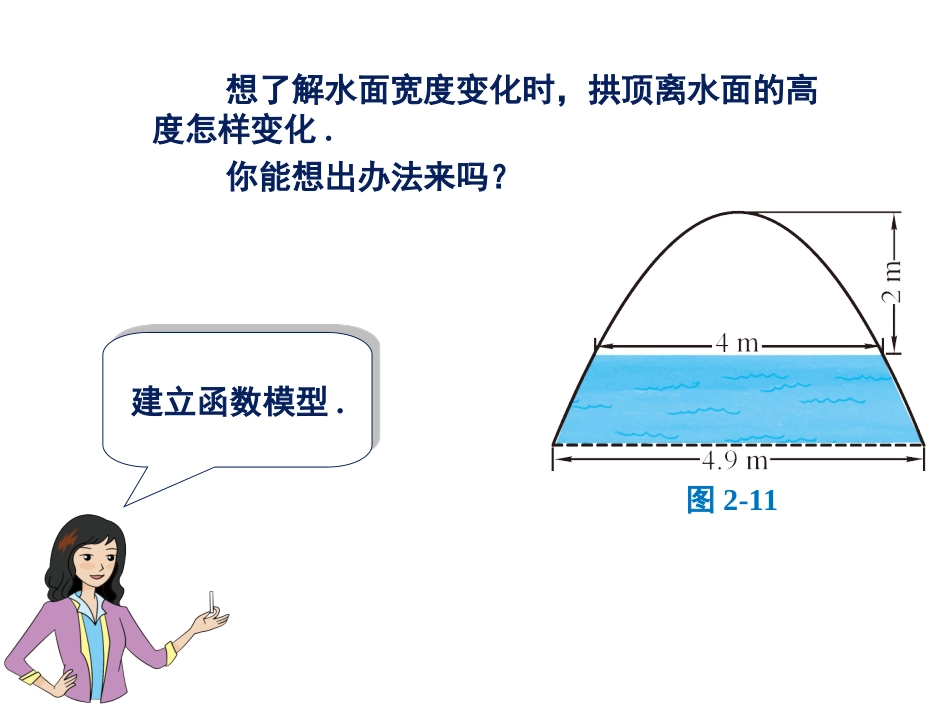
二次函数的应用本课内容本节内容2.3——2.3.1把握变量之间的依赖关系说一说一座拱桥的纵截面是抛物线的一段,拱桥的跨度是4.9m,水面宽4m时,拱顶离水面2m,如图2-11.你能想出办法来吗?建立函数模型.建立函数模型.想了解水面宽度变化时,拱顶离水面的高度怎样变化.图2-11拱桥的纵截面是抛物线,应当是某个二次函数的图象.拱桥的纵截面是抛物线,应当是某个二次函数的图象.这是什么样的函数呢?图2-11以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系.如图2-12.以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系.如图2-12.怎样建立直角坐标系比较简便呢?图2-11由于顶点坐标是(0,0),因此这个二次函数的形式为y=ax2.由于顶点坐标是(0,0),因此这个二次函数的形式为y=ax2.从图2-12看出,什么形式的二次函数,它的图象是这条抛物线呢?图2-12如何确定a是多少?图2-12已知水面宽4m时,拱顶离水面高2m,因此点A(2,-2)在抛物线上.由此得出-2=a·22,解得已知水面宽4m时,拱顶离水面高2m,因此点A(2,-2)在抛物线上.由此得出-2=a·22,解得1=.2a-这样我们可以了解到水面宽度变化时,拱顶离水面高度怎样变化.因此,,其中|x|是水面宽度的一半,y是拱顶离水面高度的相反数.21=2yx-由于拱桥的跨度为4.9m,因此自变量x的取值范围是:-2.45≤x≤2.45.现在你能求出当水面宽3m时,拱顶离水面高多少吗?水面宽3m时,,从而因此拱顶离水面高1.125m.水面宽3m时,,从而因此拱顶离水面高1.125m.3=2x2139===1.125.228y---×你是否体会到,从实际问题建立起函数模型,对于解决问题是有效的?例1用8m的铝材做成一个日字形窗框,如图2-13.试问:窗框的宽和高各为多少时,窗框的透光面积最大?最大面积是多少?(假设铝材的宽度不计)举例分析:设窗框的宽为xm,则高为,其中0