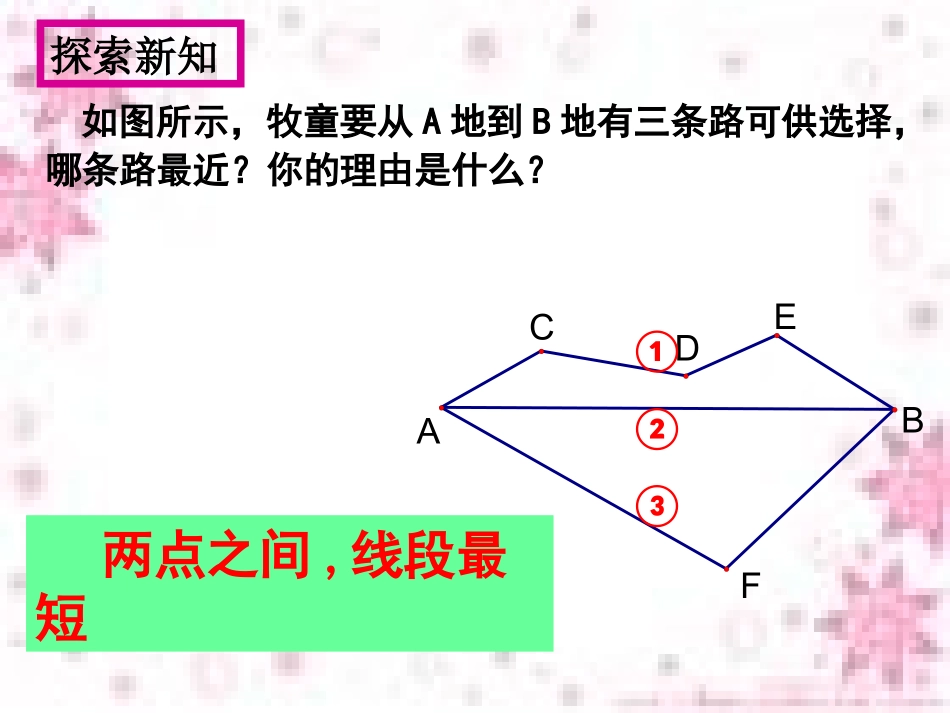
13.4课题学习最短路径问题济源市北海中学李二军济源市北海中学李二军问题1相传,古希腊亚历山大里亚城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:从图中的A地出发,到一条笔直的河边l饮马,然后到B地.到河边什么地方饮马可使他所走的路线全程最短?BAll如图所示,牧童要从A地到B地有三条路可供选择,哪条路最近?你的理由是什么?两点之间,线段最短FEDCBA①②③探索新知((一一))两点在一条直线异两点在一条直线异侧侧已知:如图,牧童从A地出发,到一条笔直的河边l处饮马,然后到B处,牧童到河边什么地方饮马,才可以使所走路径最短。P连接AB,线段AB与直线L的交点P,就是所求。l﹒﹒AB探索新知思考为什么这样做就能得到最短距离呢?根据:两点之间线段最短.((二二))两点在一条直线同侧两点在一条直线同侧已知:如图,牧童从A地出发,到一条笔直的河边l处饮马,然后到B处,牧童到河边什么地方饮马,才可以使所走路径最短。作法:(1)作点___关于直线___的对称点___;(2)连接____,与直线l相交于点C.则点C即为所求.作法:(1)作点___关于直线___的对称点___;(2)连接____,与直线l相交于点C.则点C即为所求.B·lA·B′B′CC﹒Pl﹒ABCCB·lA·A′A′问题3你能用所学的知识证明AC+BC最短吗?C′C′B·lA·B′B′CC﹒﹒AC′+C′B′>AC+CB′C′BCBAC′+C′BAC+CB>追问2回顾前面的探究过程,我们借助了什么样的方法,把“折线”问题转化为什么问题,借助什么知识找到了点C的位置,借助什么知识证明点C是使路径最短的点?牧童家在A处。现在牧童要先带马到河(图中用直线a表示)饮水,再到草地(图中用直线b表示)吃草,然后回姥姥家B处。问:牧童让马在何处饮水、吃草?abAB﹒﹒A′B′MN三、两点在两相交直线内部三、两点在两相交直线内部作____关于_____的对称点__,作____关于_____的对称点______,连接_____,分别交直线a、b于______所以______是所求的点。牧童家在A处。现在牧童要先带马到河(图中用直线a表示)饮水,再到草地(图中用直线b表示)吃草,然后回家。问:牧童让马在何处饮水?牧童家在A处。现在牧童要先带马到河(图中用直线a表示)饮水,再到草地(图中用直线b表示)吃草,然后回家。问:牧童让马在何处饮水?﹒﹒A〞AAA′A′MNaabb四、一点在两相交直线内部四、一点在两相交直线内部o作____关于_____的对称点__,作____关于_____的对称点_____,连接_____,分别交a、b于______所以______是所求的点。已知:如图A是锐角∠MON内部任意一点,在∠MON的两边OM,ON上各取一点B,C,组成三角形,使三角形周长最小.分别作点A关于OM,ON的对称点A′,A″;连接A′,A″,分别交OM,ON于点B、点C,则点B、点C即为所求.AA′A〞BCOMN11、在解决问题的过程中运用了、在解决问题的过程中运用了_____(_____(方方法法),),把不同类型的把不同类型的““折线折线””问题转化成了问题转化成了____________问题问题,,利用利用___________(___________(知识知识))找到找到了使路径最短的点。了使路径最短的点。22、体现了什么样的数学思想?、体现了什么样的数学思想?归纳总结课外作业数学书第93页15题