一元二次方程复习课件VIP免费

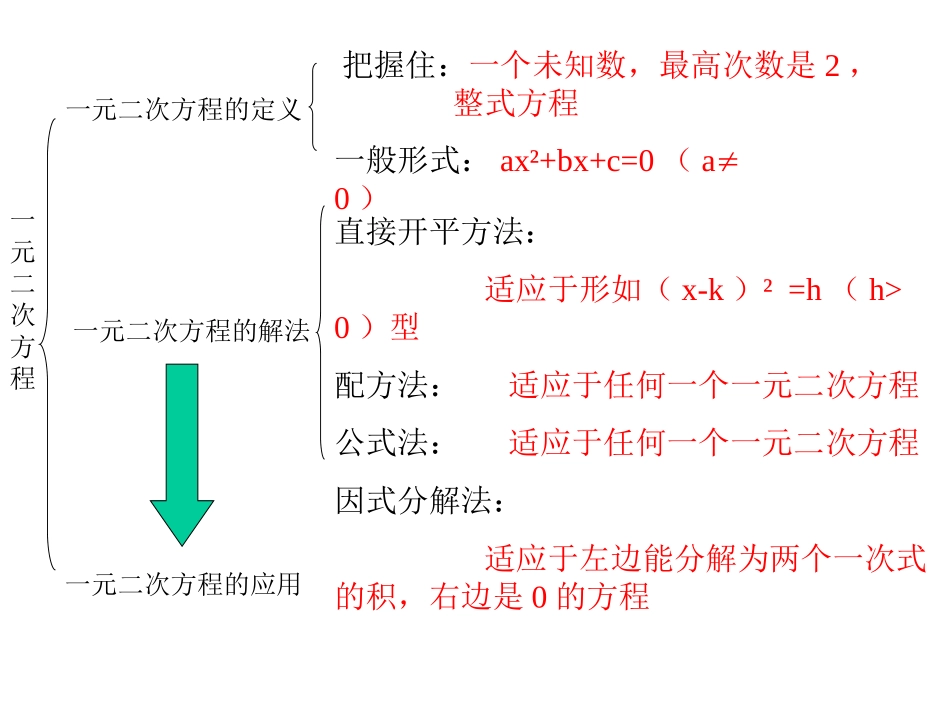
一元二次方程教学目标：1.了解一元二次方程及其相关概念，会用配方法、公式法、分解因式法解简单的一元二次方程（数字系数）2.能够利用一元二次方程解决有关的实际问题，并根据具体问题的实际意义检验结果的合理性，进一步培养学生分析问题、解决问题的意识和能力。一元二次方程一元二次方程的定义一元二次方程的解法一元二次方程的应用把握住：一个未知数，最高次数是2，整式方程一般形式：ax²+bx+c=0（a0）直接开平方法：适应于形如（x-k）²=h（h>0）型配方法：适应于任何一个一元二次方程公式法：适应于任何一个一元二次方程因式分解法：适应于左边能分解为两个一次式的积，右边是0的方程2只含有一个未知数x,并且都可以化为(a、b、c为常数，且）的形式,这样的整式a方x+bx+c程叫做一元=0a0二次方程定义：22我们把(a、b、c为常数,且a0）称为一元二次方程的一般形式，其中，，分别称为二次项、一次项、常数项，ax+bx+c=0axbxcab，分别称为二次项系数和一次项系数。一元二次方程各项及其系数：例1：指出下列方程中，那些是一元二次方程？（1）5x-6=02111x11xx(2)(x-2)(x-3)=x²-5(3)ax²+bx+c=0(4)3x-2=6x(5)(6)请说出你的判断依据2、把方程（1-x)(2-x)=3-x2化为一般形式是：___________,其二次项系数是____,一次项系数是____,常数项是____.3、方程（m-2)x|m|+3mx-4=0是关于x的一元二次方程，则（）A.m=±2B.m=2C.m=-2D.m≠±22x2-3x-1=02-3-1C一元二次方程根的判别式acb42002acbxax042acb000两不相等实根两相等实根无实根一元二次方程一元二次方程根的判式是:002acbxax判别式的情况根的情况定理与逆定理042acb042acb两个不相等实根两个相等实根无实根(无解)二、例1：不解方程，判别下列方程的根的情况（1）04322xx（3）07152xx（2）yy2491620414243422acb解：（1）=判别式的应用:所以，原方程有两个不相等的实根。说明：解这类题目时，一般要先把方程化为一般形式，求出△，然后对△进行计算，使△的符号明朗化，进而说明△的符号情况，得出结论。1、不解方程，判别方程的根的情况例2：当k取什么值时，已知关于x的方程：（1）方程有两个不相等的实根；（2）方程有两个相等的实根；（3）方程无实根；01214222kxkx解：△=9881618161224142222kkkkkk(1).当△>0，方程有两个不相等的实根,8k+9>0,即89k(2).当△=0，方程有两个相等的实根,8k+9=0,即89k(3).当△<0，方程有没有实数根,8k+9<0,即982、根据方程的根的情况确定方程的待定系数的取值范围说明：解此类题目时，也是先把方程化为一般形式，再算出△，再由题目给出的根的情况确定△的情况。从而求出待定系数的取值范围K＜配方法配方法解一元二次方程的解题过程1.把方程化成一元二次方程的一般形式2.把二次项系数化为13.把含有未知数的项放在方程的左边，不含未知数的项放在方程的右边。4.方程的两边同加上一次项系数一半的平方5.方程的左边化成完全平方的形式，方程的右边化成非负数6.利用直接开平方的方法去解公式法公式法解一元二次方程的解题过程1.把方程化成一元二次方程的一般形式2.写出方程各项的系数3.计算出b2-4ac的值，看b2-4ac的值与0的关系，若b2-4ac的值小于0，则此方程没有实数根。4.当b2-4ac的值大于、等于0时，代入求根公式计算出方程的值4240acaac22-bbbx=（）分解因式法1.移项，使方程的右边为0。2.将方程化为x（x-a）=0或x2–a2=0的形式。3.令每个因式分别为零，得到两个一元一次方程。4.解这两个一元一次方程，它们的解就是原方程的解。2222252335525()()3636549()636xxxxx2.配方法23520xx解：131x22x5766x23,5,24495757236abcbacx解：23520xx131x22x1.公式法1.解方程:(x+1)(x+2)=62.已知:(a2+b2)(a2+b2-3)=10求a2+b2的值。中考直击思考21212120,0,,xbxcaxxbcxxxxaa如果a的两个根是那么四、一元二次方程根与系数的关系以两个数x...