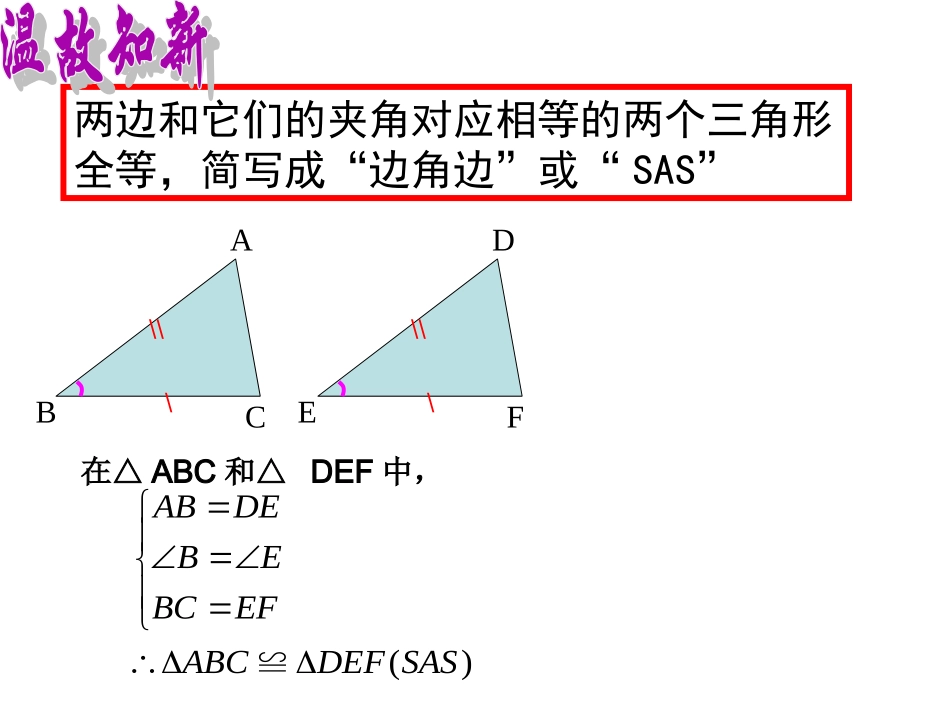
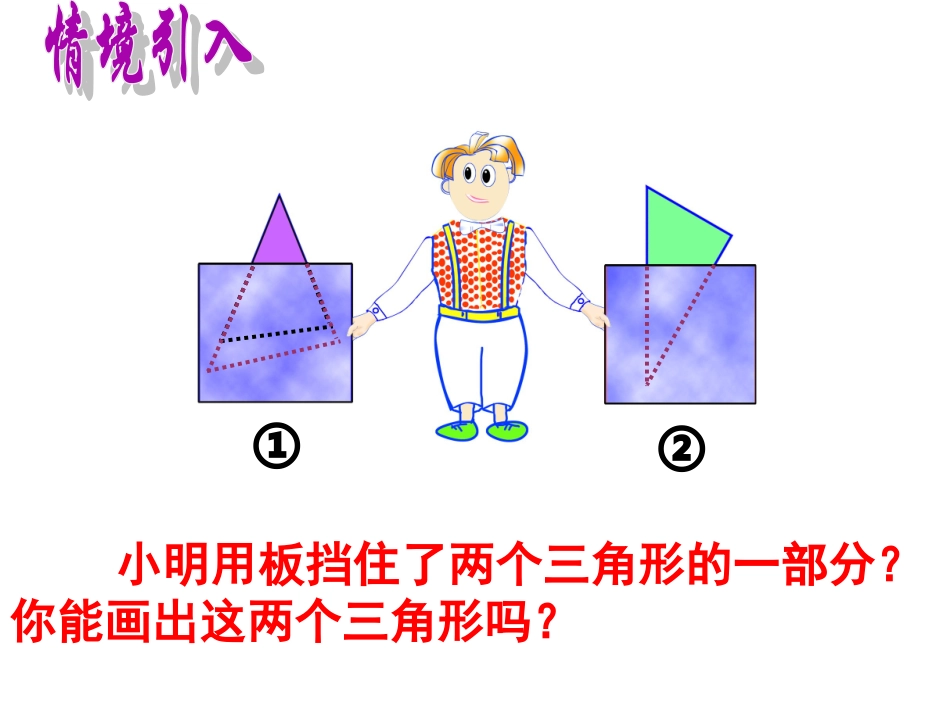
11.3探索三角形全等的条件(二)----ASA建湖县高作中学王星星两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”\\\ABC\\\DEF在△ABC和△DEF中,)(SASDEFABCEFBCEBDEAB≌小明用板挡住了两个三角形的一部分?你能画出这两个三角形吗?①②观察下面三个三角形,先猜一猜,再量一量,哪两个三角形是全等三角形?RP2.560ºQ40ºABC2.540º60ºFED2.540º60º请用量角器和刻度尺画△ABC,使AB=2cm,∠A=60º,∠B=45º。(1)画线段AB=2cm,(2)在AB的同旁,分别以A、B为顶点画∠PAB=60º,∠QBA=45º,(3)射线AP与射线BQ交于点C。QBAP60º45ºC△ABC就是所求作的三角形ABCDEF两角和它们的夹边对应相等的两个三角形全等.简写成“角边角”或“ASA”在△ABC和△DEF中,∠B=∠EBC=EF∠C=∠F△ABC≌△DEFABCDEF(ASA)AB利用“角边角”可知,带B块去,可以配到一个与原来全等的三角形玻璃。.已知:如图,AB=A’C,∠A=A’∠,∠B=C∠求证:△ABEA’CD≌△________()________()________()证明:在______和_______中∴——≌———()CDA'ABE△ABE△A’CD∠A=A’∠已知AB=A’C已知∠B=C∠已知△ABE△A’CDASAOCABD已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=C∠。求证:(1)BE=CD例1.E证明:在△ABE和△ACD中∠A=A∠(公共角)AB=AC(已知)∠B=C∠(已知)∴△ABEACD≌△(ASA)∴BE=CD(全等三角形的对应边相等)(2)BD=CE建湖县高作中学王星星ABCDEF已知:如图,点D是BC的中点,点E在AB上,点F在AC上,且DE∥AC,DF∥AB。求证:BE=DF,DE=CF例2.课本第19页ABCDE12如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?探索三角形全等的条件ASASASABCDEF一般地,SSA不能判定两三角形全等,那么AAS能判定两三角形全等吗?建湖县高作中学王星星用直尺和圆规作符合条件的△ABC课本第18页