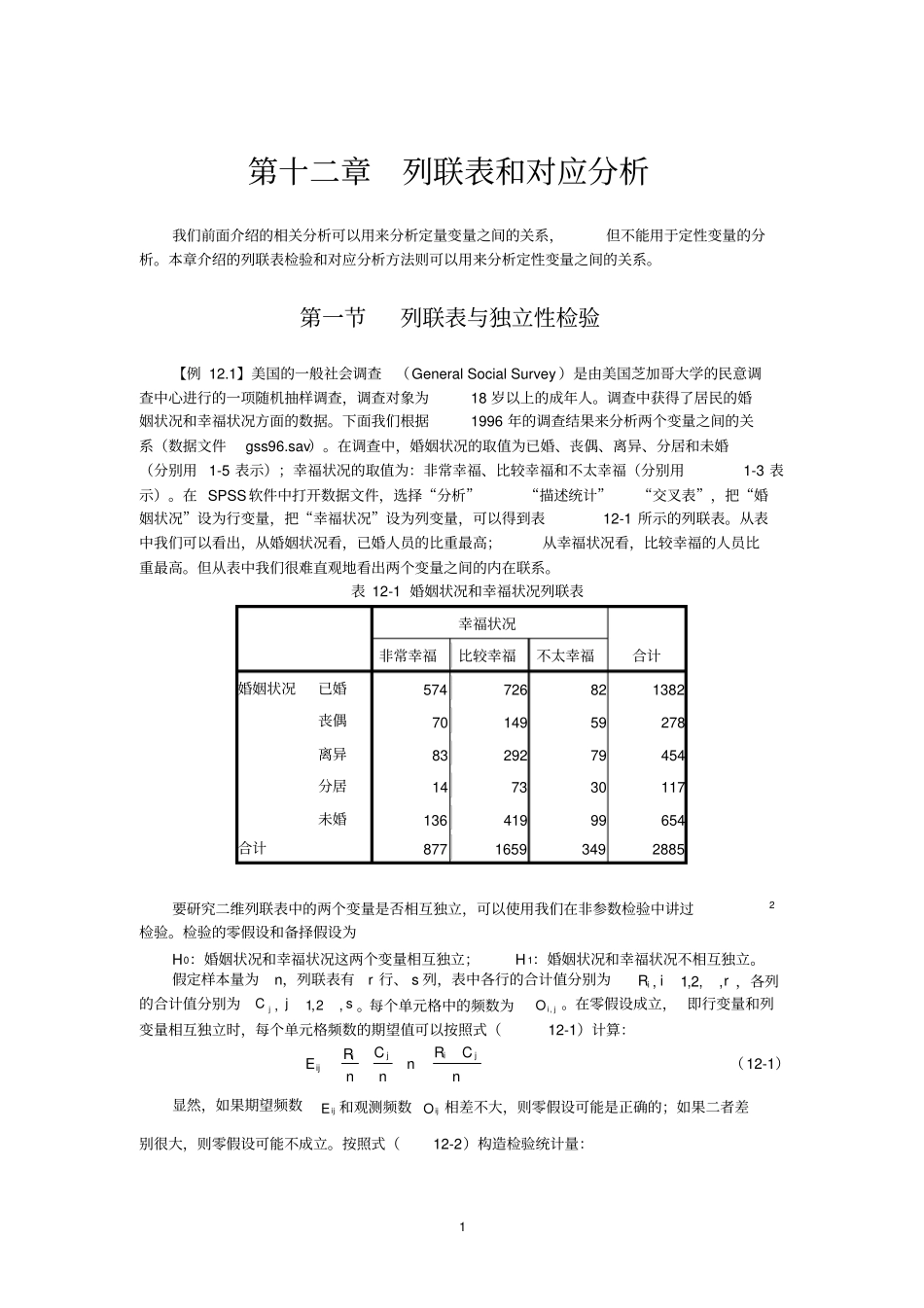
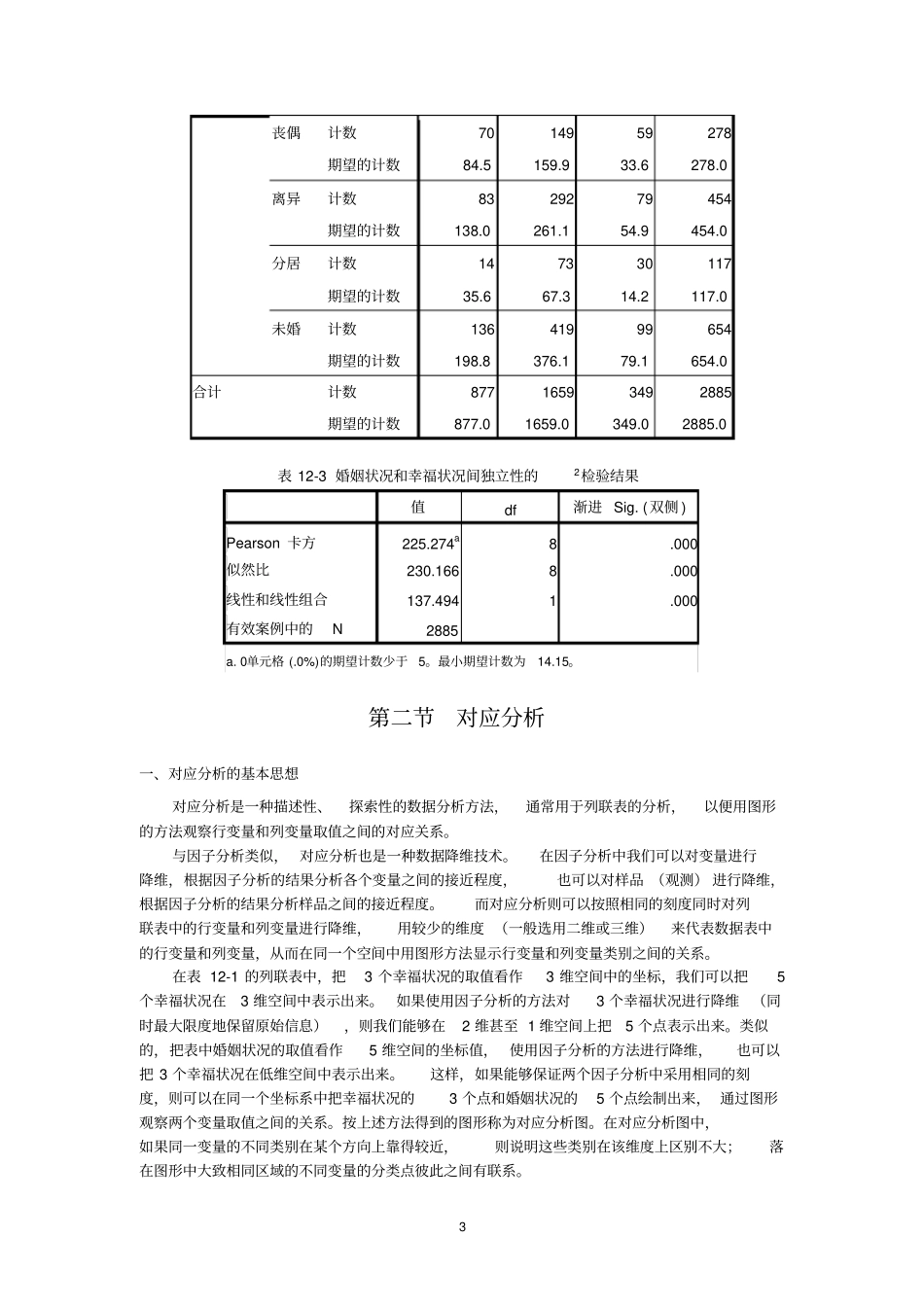
1 第十二章列联表和对应分析我们前面介绍的相关分析可以用来分析定量变量之间的关系,但不能用于定性变量的分析。本章介绍的列联表检验和对应分析方法则可以用来分析定性变量之间的关系。第一节列联表与独立性检验【例 12.1】美国的一般社会调查(General Social Survey )是由美国芝加哥大学的民意调查中心进行的一项随机抽样调查,调查对象为18 岁以上的成年人。调查中获得了居民的婚姻状况和幸福状况方面的数据。下面我们根据1996 年的调查结果来分析两个变量之间的关系(数据文件gss96.sav)。在调查中,婚姻状况的取值为已婚、丧偶、离异、分居和未婚(分别用 1-5 表示);幸福状况的取值为:非常幸福、比较幸福和不太幸福(分别用1-3 表示)。在 SPSS软件中打开数据文件,选择“分析”“描述统计”“交叉表”,把“婚姻状况”设为行变量,把“幸福状况”设为列变量,可以得到表12-1 所示的列联表。从表中我们可以看出,从婚姻状况看,已婚人员的比重最高;从幸福状况看,比较幸福的人员比重最高。但从表中我们很难直观地看出两个变量之间的内在联系。表 12-1 婚姻状况和幸福状况列联表幸福状况合计非常幸福比较幸福不太幸福婚姻状况已婚574 726 82 1382 丧偶70 149 59 278 离异83 292 79 454 分居14 73 30 117 未婚136 419 99 654 合计877 1659 349 2885 要研究二维列联表中的两个变量是否相互独立,可以使用我们在非参数检验中讲过2检验。检验的零假设和备择假设为H0:婚姻状况和幸福状况这两个变量相互独立;H 1:婚姻状况和幸福状况不相互独立。假定样本量为n,列联表有r 行、 s 列,表中各行的合计值分别为riRi,,2,1,,各列的合计值分别为sjC j,2,1,。每个单元格中的频数为jiO , 。在零假设成立, 即行变量和列变量相互独立时,每个单元格频数的期望值可以按照式(12-1)计算:nCRnnCnREjijiij(12-1)显然,如果期望频数ijE 和观测频数ijO 相差不大,则零假设可能是正确的;如果二者差别很大,则零假设可能不成立。按照式(12-2)构造检验统计量:2 risjijijijEEO1122)((12-2)在零假设成立时, 该统计量近似服从自由度为)1)(1(sr的2 分布。 当该统计量的值很大(或 p 值很小)时,就可以拒绝零假设,认为这两个变量不相互独立。下面我们用SPSS软件来检验婚姻状况与幸福状况的独立性。首先重复绘制列联表的步骤,在 SPSS软件中打开数据文件,选择“分析”“描述统计”“交叉表...