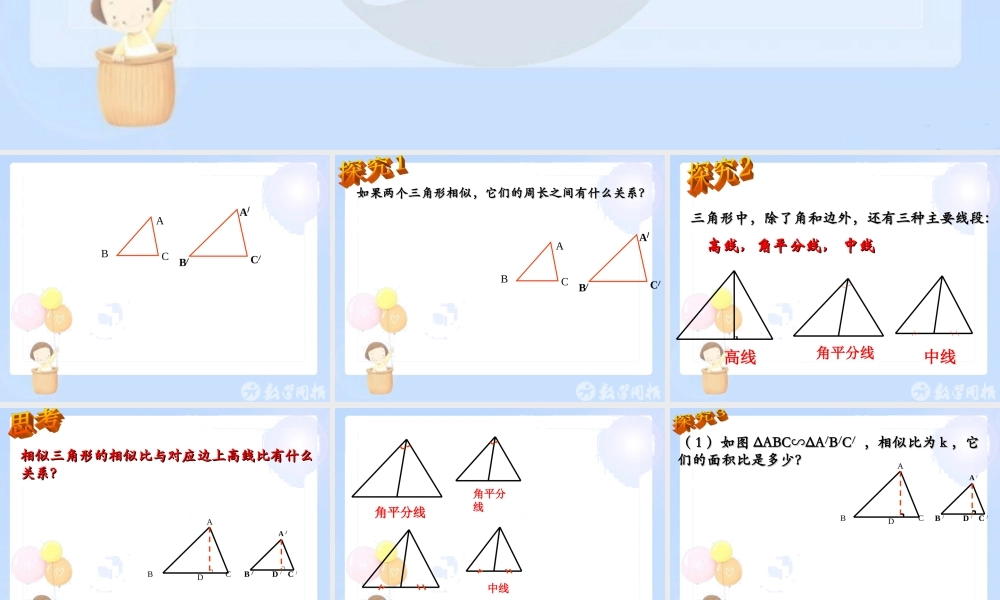
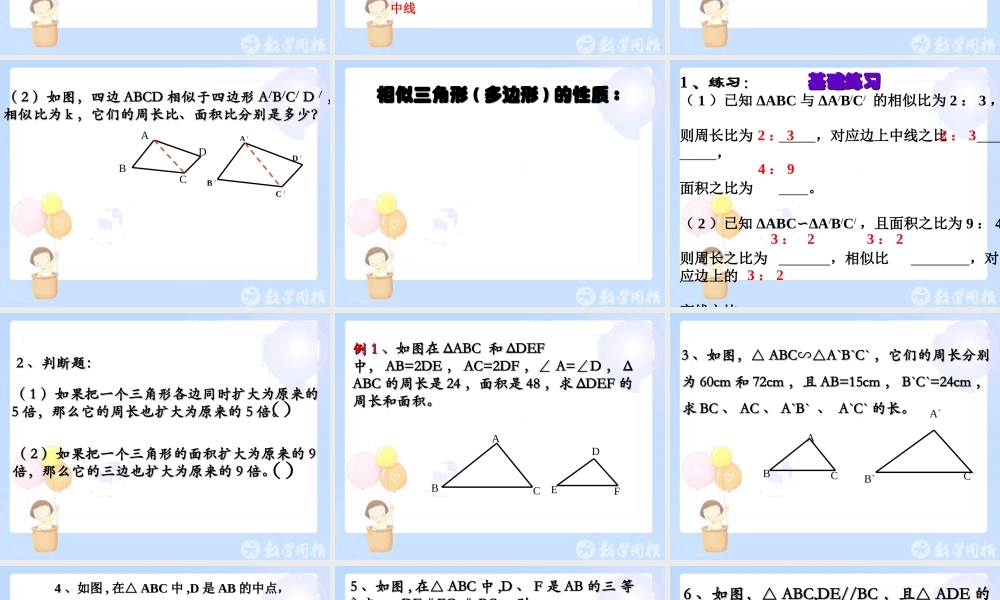
27.2 27.2 相似三角形相似三角形(( 第第 66 课时课时 ))ABCA/B/C/如果两个三角形相似,它们的周长之间有什么关系?如果两个三角形相似,它们的周长之间有什么关系?ABCA/B/C/三角形中,除了角和边外,还有三种主要线段:三角形中,除了角和边外,还有三种主要线段:高线,角平分线, 中线高线,角平分线, 中线高线角平分线中线相似三角形的相似比与对应边上高线比有什么相似三角形的相似比与对应边上高线比有什么关系?关系?ABCDA /B /C /D /角平分线角平分线中线中线(( 11 )如图)如图 ΔABC∽ΔAΔABC∽ΔA//BB//CC// ,相似比为,相似比为 kk ,它,它们的面积比是多少?们的面积比是多少?A B CDA /B /C /D /(( 22 )如图,四边)如图,四边 ABCDABCD 相似于四边形相似于四边形 AA//BB//CC// D D // ,,相似比为相似比为 kk ,它们的周长比、面积比分别是多少?,它们的周长比、面积比分别是多少?ABCDA /B /C /D /相似三角形相似三角形 (( 多边形多边形 )) 的性质的性质 ::1 、练习:( 1 )已知 ΔABC 与 ΔA/B/C/ 的相似比为 2 : 3 ,则周长比为 ,对应边上中线之比 ,面积之比为 。( 2 )已知 ΔABCΔA∽/B/C/ ,且面积之比为 9 : 4 ,则周长之比为 ,相似比 ,对应边上的高线之比 。 2 : 34 : 93 : 23 : 23 : 22 : 3基础练习基础练习22 、判断题:、判断题:(( 11 )如果把一个三角形各边同时扩大为原来的)如果把一个三角形各边同时扩大为原来的55 倍,那么它的周长也扩大为原来的倍,那么它的周长也扩大为原来的 55 倍。倍。()(( 22 )如果把一个三角形的面积扩大为原来的)如果把一个三角形的面积扩大为原来的 99倍,那么它的三边也扩大为原来的倍,那么它的三边也扩大为原来的 99 倍。倍。()例例 11 、、如图在如图在 ΔABC ΔABC 和和 ΔDEFΔDEF中,中, AB=2DEAB=2DE ,, AC=2DFAC=2DF ,,∠∠ A=∠DA=∠D ,, ΔΔABCABC 的周长是的周长是 2424 ,面积是,面积是 4848 ,求,求 ΔDEFΔDEF 的的周长和面积。周长和面积。AB CDEF33 、如图,△、如图,△ ABC∽△A`B`C`ABC∽△A`B`C` ,它们的周长分别,它们的周长分别为为 60cm60cm 和和 72cm72cm ,且,且 AB=15cmAB=15cm ,, B`C`=24cmB`C`=24cm ,,求求 BCBC 、、 ACAC 、、 A`B` A`B` 、 、 A`C`A`C`...