阅读与思考割圆术VIP免费

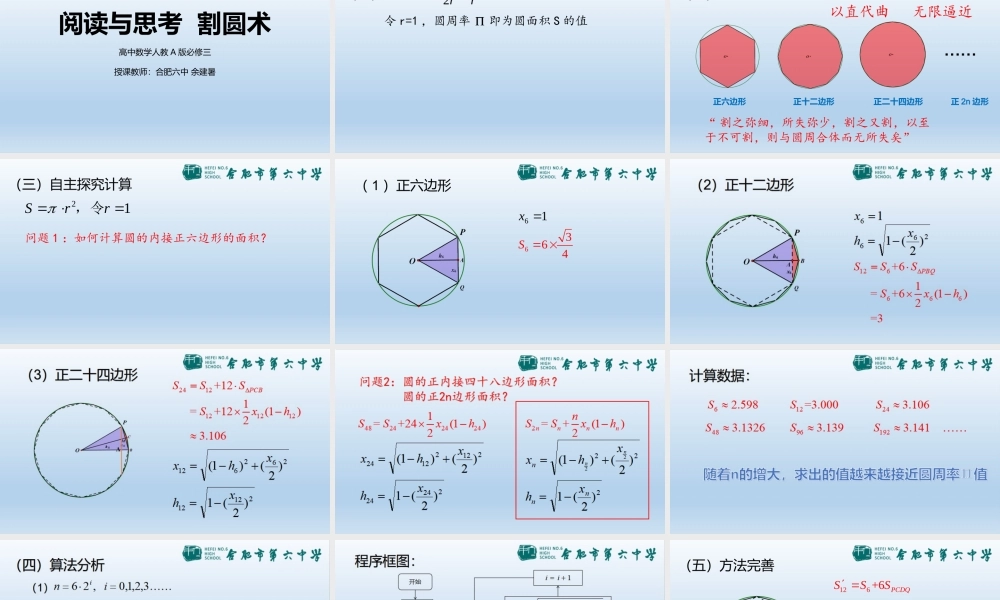
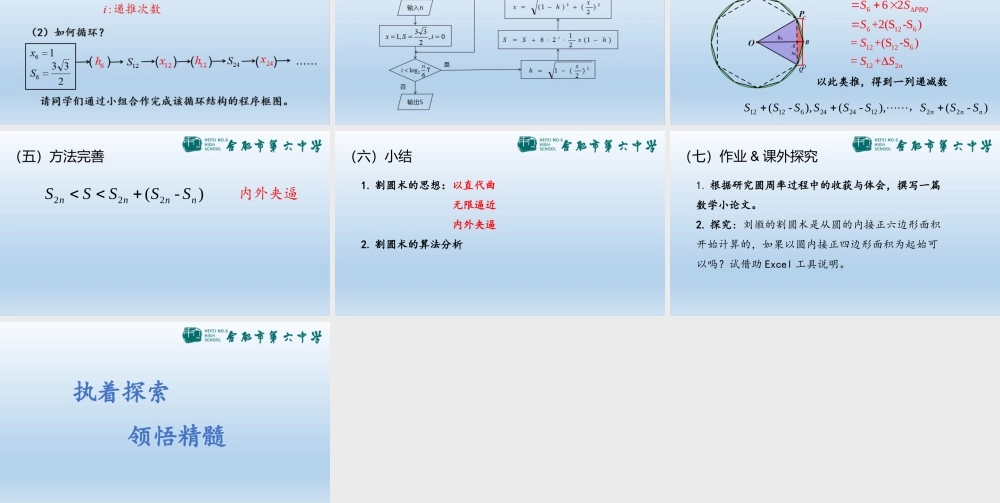
阅读与思考 割圆术高中数学人教 A 版必修三授课教师：合肥六中 余建暑（一）关于22rSrC  令 r=1 ，圆周率 Π 即为圆面积 S 的值 正六边形 正十二边形 正二十四边形……“ 割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣” 正 2n 边形（二）割圆术的原理以直代曲 无限逼近（三）自主探究计算 12rrS，令问题 1 ：如何计算圆的内接正六边形的面积？（ 1 ）正六边形16 x6364S  （五）方法完善 CD1266612612126122+66 2+2(S -S )= +(S -S )= +PCDQPBQnSSSSSSSSS  以此类推，得到一列递减数)-(),-(),-(2212242461212nnnSSSSSSSSS，（五）方法完善 )-(222nnnnSSSSS内外夹逼（六）小结 1. 割圆术的思想：以直代曲 无限逼近 内外夹逼2. 割圆术的算法分析（七）作业 & 课外探究 1. 根据研究圆周率过程中的收获与体会，撰写一篇数学小论文。2. 探究：刘徽的割圆术是从圆的内接正六边形面积开始计算的，如果以圆内接正四边形面积为起始可以吗？试借助 Excel 工具说明。执着探索 领悟精髓