第五、六讲-轴向拉压变形VIP免费

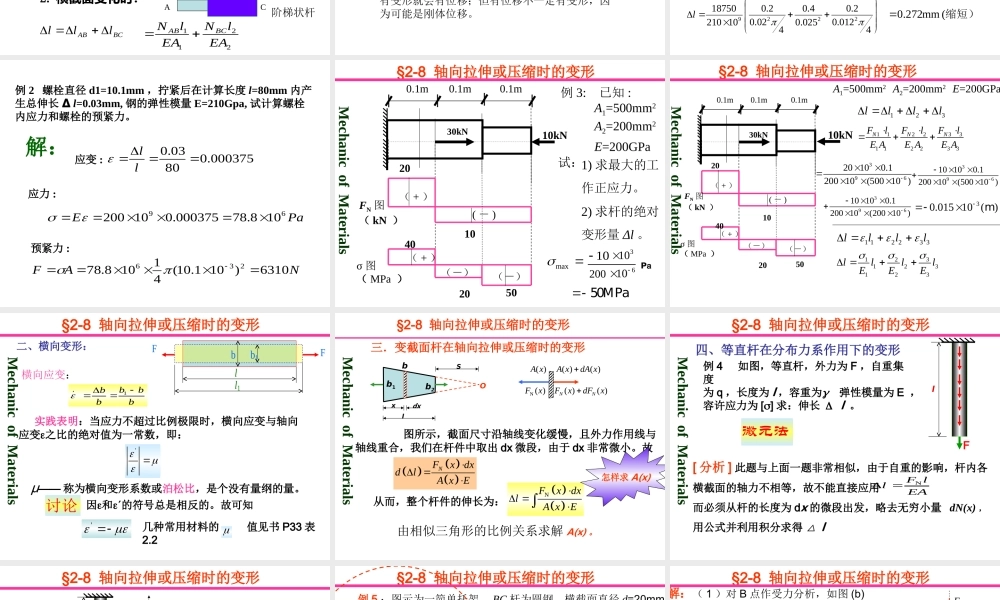
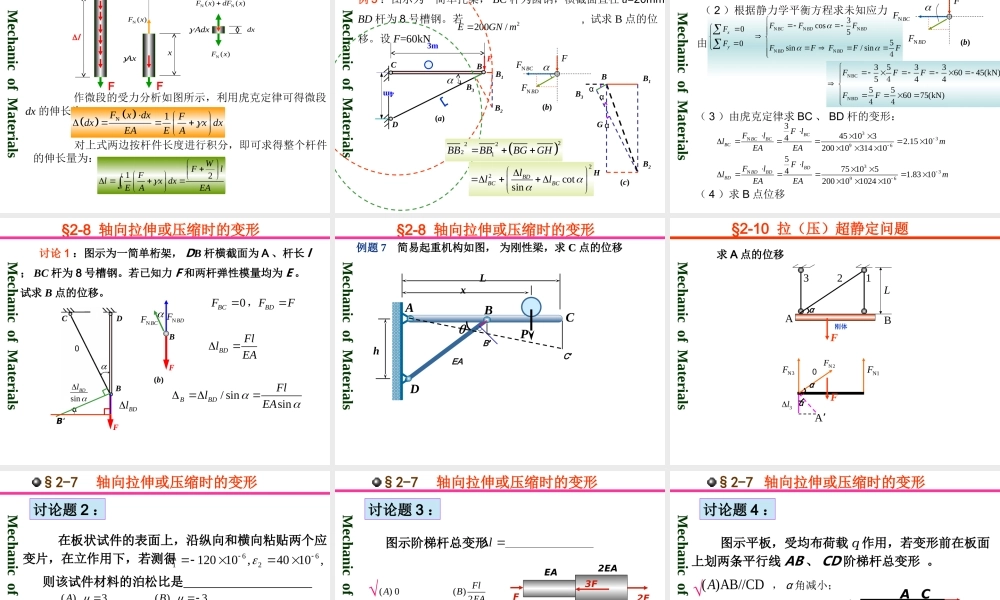
§2-8 轴向拉伸或压缩时的变形§2-10 拉（压）超静定问题Mechanic of Materials第五、六讲内容目录§2-12 应力集中的概念§2-9 轴向拉伸或压缩时的变形能 拉压杆的变形与位移、超静定问题 教学要求： 1 、超静定问题的基本方法（拉压） ； 2 、熟练掌握纵向、横向应变，虎克定律和材料的弹性模量 E 这些基本概念和定律； 3 、掌握求拉压杆的变形。 重点：应变、虎克定律 难点：求拉压杆系变形后的位置 学时安排： 2 学时教学内容：第五、六讲的内容、要求、重难点Mechanic of Materials l1 b §2-8 轴向拉伸或压缩时的变形一、等直杆在轴向拉伸或压缩时的变形直杆在外力 F 作用前后的情况如图中所示： F F b1 l 1 、轴向变形lll1Mechanic of Materials轴向绝对变形 NF llEA      当轴力、面积、E轴线方向线应变： ll横截面上应力： NFA 虎克定律： ------------ 虎克定律的两种表达形式 物理意义：即当应力不超过比例极限时，杆件的伸长 l 与 F和杆件的原长度成正比，与横截面面积 A 成反比。式中： EA—— 杆件的抗拉（压）刚度。 EA 越大，  l 越小 Mechanic of MaterialsF F b b1 l l1 NFllA NF llEA  NFlElEAENEAFl§2-8 轴向拉伸或压缩时的变形 2 ）构件的工作应力p（线弹性范围内）；3 ）轴力 N 、横截面面积 A 为常量——等直杆两端受轴向力；讨论：1. 轴力变化时3P1P1 ） L 为“ +” 时伸长，为“ -” 时缩短，符号规定与轴力一致。拉为“ +” ，压为“ -” 。BCABlllEAlNEAlNBCAB21 2. 横截面变化时：BC1l2l2PACAB阶梯状杆BCABlll2. 公式的应用范围与注意事项2211EAlNEAlNBCAB 若轴力 FN=FN(x) ，或 AN=AN(x) 则lNxEAdxxFL)()(3 、 位移的计算 物体受外力后会发生形状和尺寸的改变，称为物体的变形，物体变形后，在物体上一些点、线、面会发生空间位置的改变。物体点、线、面空间位置的改变称位移。有变形就会有位移；但有位移不一定有变形，因为可能是刚体位移。 例 1 图示杆， 1 段为直径 d1=20mm 的圆杆， 2段为边长 a=25mm 的方杆， 3 段为直径 d3=12mm 的圆杆。已知 2 段杆内的应力 σ2=-30MPa ， E=210GPa ，求整个杆的伸长△ L解:kN75.18)N1025()1030(62622...