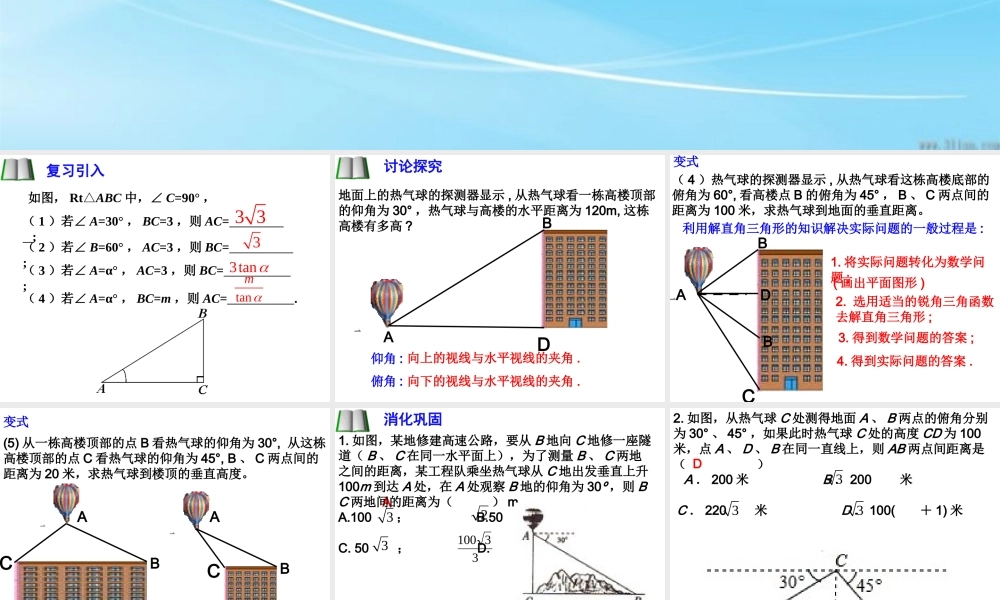
28.2 解直角三角形( 2 ) 复习引入如图, Rt△ABC 中,∠ C=90° ,( 1 )若∠ A=30° , BC=3 ,则 AC= ;( 2 )若∠ B=60° , AC=3 ,则 BC= ;( 3 )若∠ A=α° , AC=3 ,则 BC= ;( 4 )若∠ A=α° , BC=m ,则 AC= .3 333tantanm讨论探究仰角 :俯角 :向上的视线与水平视线的夹角 .向下的视线与水平视线的夹角 .地面上的热气球的探测器显示 , 从热气球看一栋高楼顶部的仰角为 30° ,热气球与高楼的水平距离为 120m, 这栋高楼有多高 ?BAD( 1 )空中的热气球的探测器显示 , 从热气球看一栋高楼顶部的仰角为 30°, 看这栋高楼底部的俯角为 60°, 热气球与高楼的水平距离为 120m, 这栋高楼有多高 ?ACD( 2 )空中的热气球的探测器显示 , 从热气球看一栋高楼顶部的仰角为 30°, 看这栋高楼底部的俯角为 60°, 这栋楼高 300 米,求热气球与高楼的水平距离。BB利用解直角三角形的知识解决实际问题的一般过程是 :1. 将实际问题转化为数学问题 ;( 画出平面图形 )2. 选用适当的锐角三角函数去解直角三角形 ;3. 得到数学问题的答案 ;4. 得到实际问题的答案 .变式( 3 )空中的热气球的探测器显示 , 从热气球看一栋高楼顶部的仰角为 45°, 看这栋高楼底部的俯角为 60°, 这栋楼高 300 米,求热气球与高楼的水平距离。( 4 )热气球的探测器显示 , 从热气球看这栋高楼底部的俯角为 60°, 看高楼点 B 的俯角为 45° , B 、 C 两点间的距离为 100 米,求热气球到地面的垂直距离。 (5) 从一栋高楼顶部的点 B 看热气球的仰角为 30°, 从这栋高楼顶部的点 C 看热气球的仰角为 45°, B 、 C 两点间的距离为 20 米,求热气球到楼顶的垂直高度。ACB(1)ACB(2)变式 A1. 如图,某地修建高速公路,要从 B 地向 C 地修一座隧道( B 、 C 在同一水平面上),为了测量 B 、 C 两地之间的距离,某工程队乘坐热气球从 C 地出发垂直上升100m 到达 A 处,在 A 处观察 B 地的仰角为 30º ,则 BC 两地间的距离为( ) m 。A.100 ; B.50 ; C. 50 ; D. 33消化巩固233100 D2. 如图,从热气球 C 处测得地面 A 、 B 两点的俯角分别为 30° 、 45° ,如果此时热气球 C 处的高度 CD 为 100米,点 A 、 D 、 B 在同一直线上,则 AB 两点间距离是( ) A . 200 ...