§7简单几何体的面积和体积VIP免费

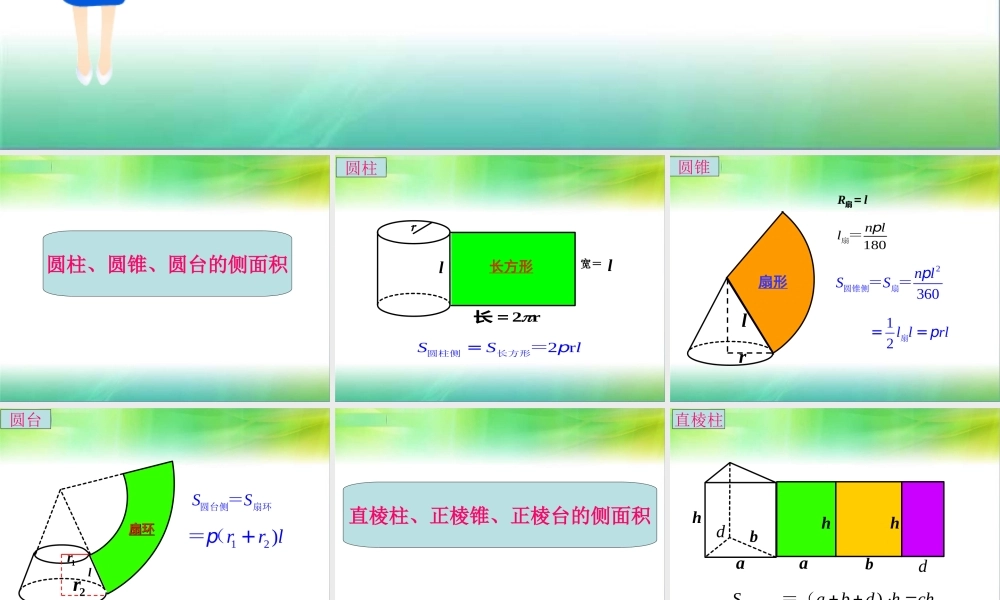
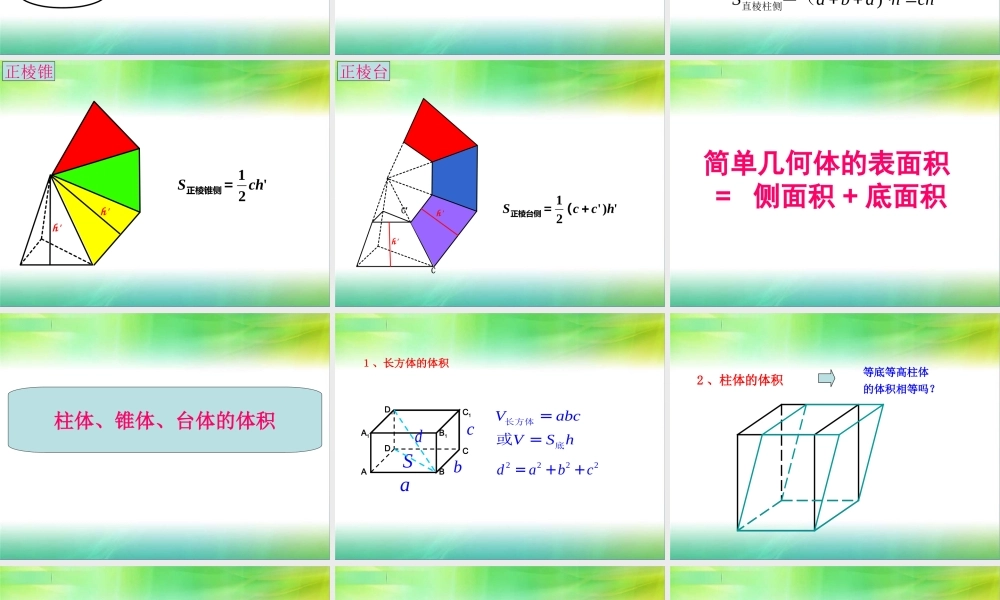
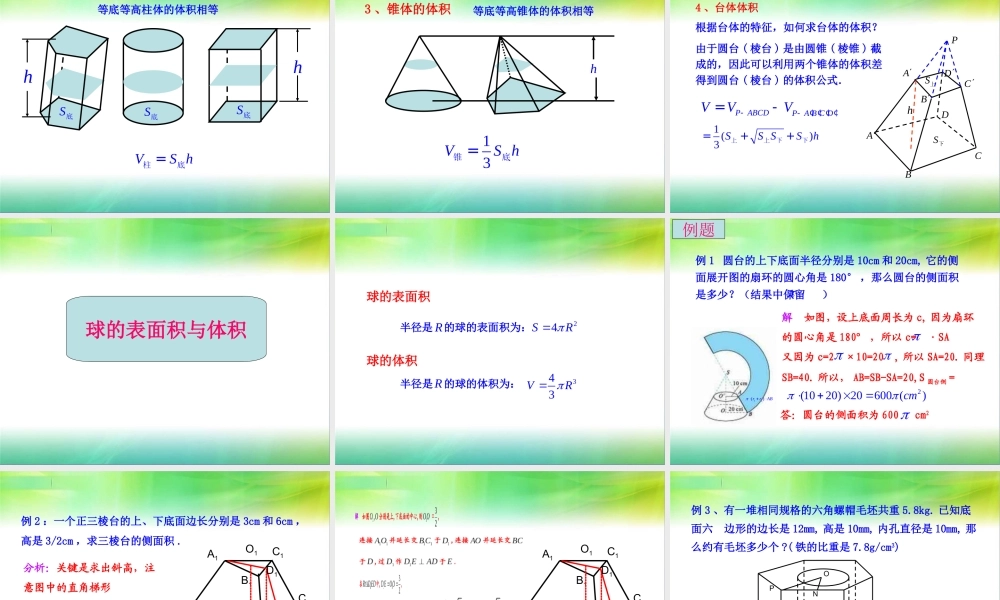
§7 简单几何体的面积和体积圆柱、圆锥、圆台的侧面积rlr2长＝宽＝ l2 rSSlp=圆柱侧长方形＝长方形圆柱rl180n llp扇＝lR ＝扇扇形2360n lSSp圆锥侧扇＝＝12 l lrlp==扇圆锥1r2rl扇环扇环SS圆台侧扇环＝12)rr lp+＝（圆台直棱柱、正棱锥、正棱台的侧面积)  Sabdhch直棱柱侧＝（habdabhhd直棱柱h'h''21 chS＝正棱锥侧正棱锥h'h'')'21hccS（＝正棱台侧CC′正棱台简单几何体的表面积= 侧面积 + 底面积柱体、锥体、台体的体积DABCD1A1B1C1abcSdVabcVS h==长方体底或2222dabc=++１、长方体的体积等底等高柱体的体积相等吗？2 、柱体的体积等底等高柱体的体积相等VS h=柱底hS底S底S底h3 、锥体的体积等底等高锥体的体积相等h13VS h=锥底4 、台体体积由于圆台 ( 棱台 ) 是由圆锥 ( 棱锥 ) 截成的，因此可以利用两个锥体的体积差得到圆台 ( 棱台 ) 的体积公式．根据台体的特征，如何求台体的体积？ABABCDCDPS下S上hPABCDPA B C DVVV¢ ¢ ¢ ¢--=-1 ()3 SS SSh=++下下上上球的表面积与体积球的体积球的表面积半径是 的球的表面积为：R24SR半径是 的球的体积为：R343VR例 1 圆台的上下底面半径分别是 10cm 和 20cm, 它的侧面展开图的扇环的圆心角是 180° ，那么圆台的侧面积是多少？（结果中保留 ）12()rrAB 解 如图，设上底面周长为 c, 因为扇环的圆心角是 180° ，所以 c= ·SA又因为 c=2 ×10=20 , 所以 SA=20. 同理SB=40. 所以， AB=SB-SA=20,S 圆台侧 =2(1020)20600 ()cm答：圆台的侧面积为 600 cm2例题B1ABCC1A1例 2 ：一个正三棱台的上、下底面边长分别是 3cm 和 6cm ，高是 3/2cm ，求三棱台的侧面积 . 分析：关键是求出斜高，注意图中的直角梯形O1ODD1EB1ABCC1A1O1ODD1EONP例 3 、有一堆相同规格的六角螺帽毛坯共重 5.8kg. 已知底面六 边形的边长是 12mm, 高是 10mm, 内孔直径是 10mm, 那么约有毛坯多少个 ?( 铁的比重是 7.8g/cm3) 分析：六角螺帽毛坯的体积是一个正六棱柱的体积与一个圆柱的体积的差 .解 :V 正六棱柱 =3×122× ×10≈3.74×103(mm3) V 圆柱 =3.14×52×10≈0.785×103(mm3) 毛坯的体积 V=3.74×103-0.785×103 ≈2.96×103(mm3)=2.96(cm3) 约有毛坯： 5.8×103÷(7.8×2.96)≈2.5×102( 个 ) 答 : 这堆毛坯约有 250 个 .ONP32例 4 、...