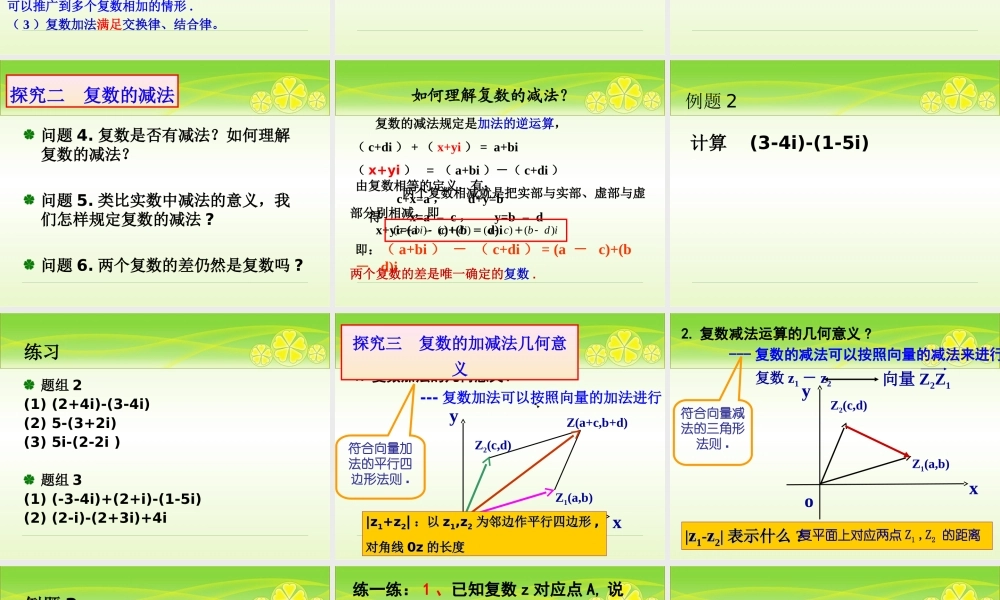
3.2.1 复数代数形式的加减运算及其几何意义 执教人:刘曼梨(3) 复数的几何意义是什么?(1) 复数的代数形式?(2) 复数相等的充要条件?z=a+bi (a , b ∈R) z=a+bi(a,b∈R)复平面上的点 Z(a,b) 向量 OZ z1=a+bi(a,b∈R) 与 z2=c+di(c,d∈R)相等的充要条件是 a=c 且 b=d知识回顾练习(1) 已知 z=5-3i, 则︱ z ︱ =( )(2) a=(1,2),b=(-2,1), 则a+b=( ) 问题 1. 复数的加法法则是如何进行的?问题 2. 两个复数的和仍然是复数吗?问题 3. 复数的加法满足交换律,结合律吗?探究一 复数的加法一、加、减法运算法则 1. 复数的加法法则:设 z1=a+bi , z2=c+di (a 、 b 、 c 、 dR)∈是任意两复数,那么它们的和:( a+bi)+(c+di)=(a+c)+(b+d)i说明 :( 1 )复数的加法运算法则是一种规定 . 当 b=0 , d=0时与实数加法法则保持一致 .( 2 )两个复数的和仍然是一个复数 , 对于复数的加法可以推广到多个复数相加的情形 .( 3 )复数加法满足交换律、结合律。例题 1计算( 1+2i ) +(-2+i) 练习题组 1. 计算(1) (2+4i)+(3-4i)(2) 3+(-1-i)(3) -3i+(i-1)(4) (5-6i)+(-2-i)+(3+4i)问题 4. 复数是否有减法?如何理解复数的减法?问题 5. 类比实数中减法的意义,我们怎样规定复数的减法 ?问题 6. 两个复数的差仍然是复数吗 ?探究二 复数的减法如何理解复数的减法? 复数的减法规定是加法的逆运算,( c+di ) + ( x+yi ) = a+bi ( x+yi ) = ( a+bi )-( c+di )由复数相等的定义,有:c+x=a , d+y=b得 x=a - c , y=b - dx+yi=(a - c)+(b - d)i即:( a+bi ) - ( c+di ) = (a - c)+(b - d)i两个复数的差是唯一确定的复数 . 两个复数相减就是把实部与实部、虚部与虚部分别相减,即()()()()abicdiacbd i+-+=-+-计算 (3-4i)-(1-5i)例题 2 练习题组 2(1) (2+4i)-(3-4i)(2) 5-(3+2i)(3) 5i-(2-2i )题组 3(1) (-3-4i)+(2+i)-(1-5i)(2) (2-i)-(2+3i)+4ixoyZ1(a,b)Z2(c,d)Z(a+c,b+d)符合向量加法的平行四边形法则 .1. 复数加法的几何意义?|z|z11+z+z22|| ::以以 zz11,z,z22 为邻边作平行四边形为邻边作平行四边形 ,,对角线对角线 0z0z 的长度的长度探究三 复数的加减法几何意义--- 复数加法可以按照向量的加法进行xoyZ1(a,b)Z2(c,d)复数 z1 - z2向量 Z2Z1符合向量减法的三角形法则...