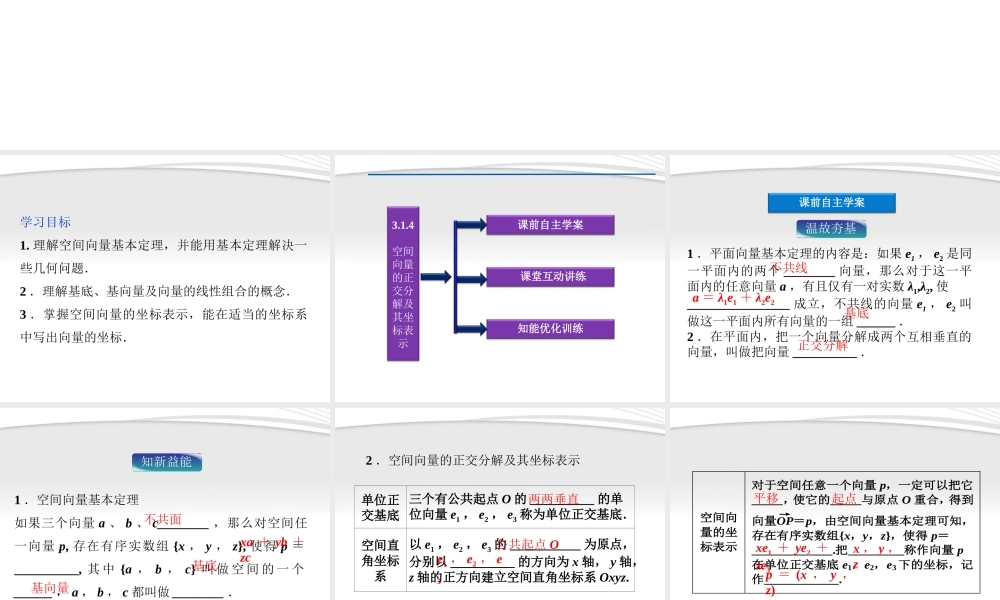
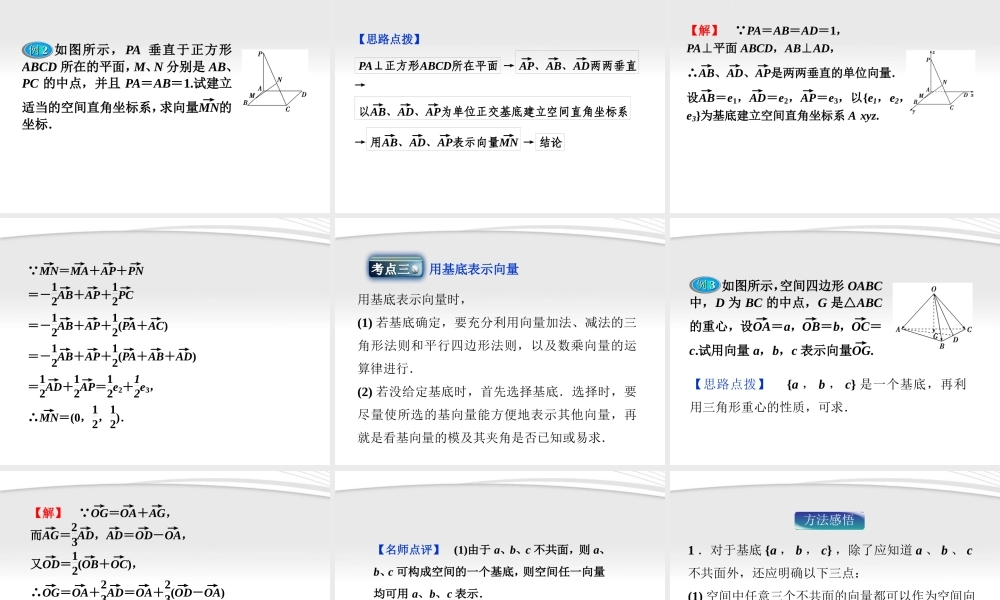
3 . 1.4 空间向量的正交分解及其坐标表示学习目标1. 理解空间向量基本定理,并能用基本定理解决一些几何问题.2 .理解基底、基向量及向量的线性组合的概念.3 .掌握空间向量的坐标表示,能在适当的坐标系中写出向量的坐标.课堂互动讲练知能优化训练3.1.4空间向量的正交分解及其坐标表示课前自主学案课前自主学案温故夯基1 .平面向量基本定理的内容是:如果 e1 , e2 是同一平面内的两个 ________ 向量,那么对于这一平面内的任意向量 a ,有且仅有一对实数 λ1,λ2, 使________________ 成立,不共线的向量 e1 , e2 叫做这一平面内所有向量的一组 ______ .2 .在平面内,把一个向量分解成两个互相垂直的向量,叫做把向量 __________ .不共线基底正交分解a = λ1e1 + λ2e2知新益能1 .空间向量基本定理如果三个向量 a 、 b 、 c________ ,那么对空间任一向量 p, 存在有序实数组 {x , y , z}, 使得 p =__________, 其 中 {a , b , c} 叫 做 空 间 的 一 个______ , a , b , c 都叫做 ________ .不共面基底基向量xa + yb +zc2 .空间向量的正交分解及其坐标表示单位正交基底三个有公共起点 O 的 __________ 的单位向量 e1 , e2 , e3 称为单位正交基底.空间直角坐标系以 e1 , e2 , e3 的 ___________ 为原点,分别以 __________ 的方向为 x 轴, y 轴,z 轴的正方向建立空间直角坐标系 Oxyz.两两垂直公共起点 Oe1 , e2 , e3空间向量的坐标表示 对于空间任意一个向量 p,一定可以把它_____,使它的_____与原点 O 重合,得到向量OP→ =p,由空间向量基本定理可知,存在有序实数组{x,y,z},使得 p=_____________.把_________称作向量 p在单位正交基底 e1,e2,e3 下的坐标,记作____________. 平移起点x , y ,zp = (x , y ,z)xe1 + ye2 +ze31 .空间的基底是惟一的吗?提示:由空间向量基本定理可知,任意三个不共面向量都可以组成空间的一个基底,所以空间的基底有无数个,因此不惟一.2 .空间向量基本定理中,当 z = 0 时,是什么定理?当 y = z = 0 时,是什么定理?提示:平面向量基本定理;共线定理.问题探究课堂互动讲练基底的判断考点突破判断三个向量能否作为基底,关键是判断它们是否共面,若从正面判断难以入手,可以用反证法结合共面向量定理或...