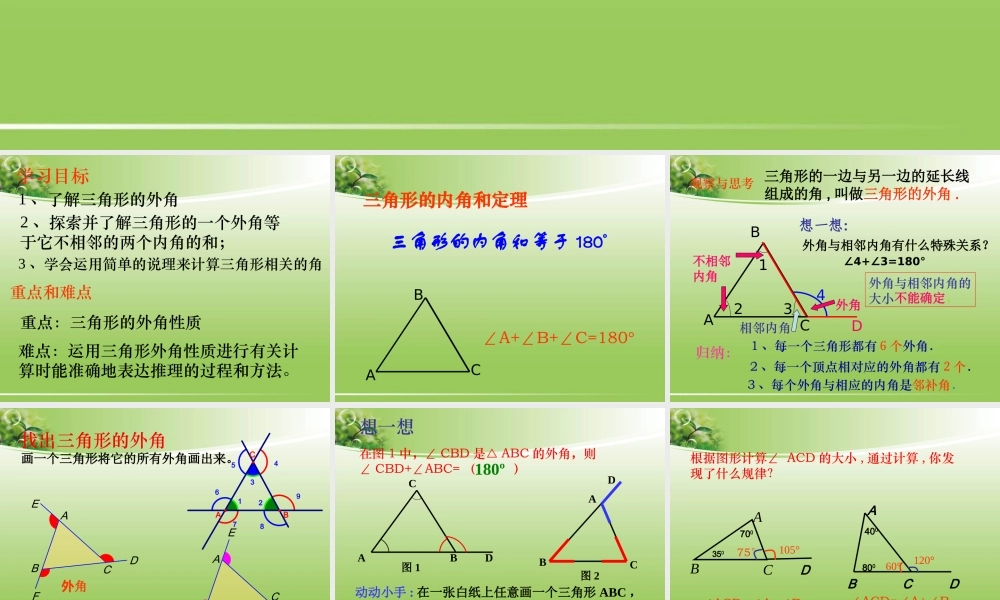
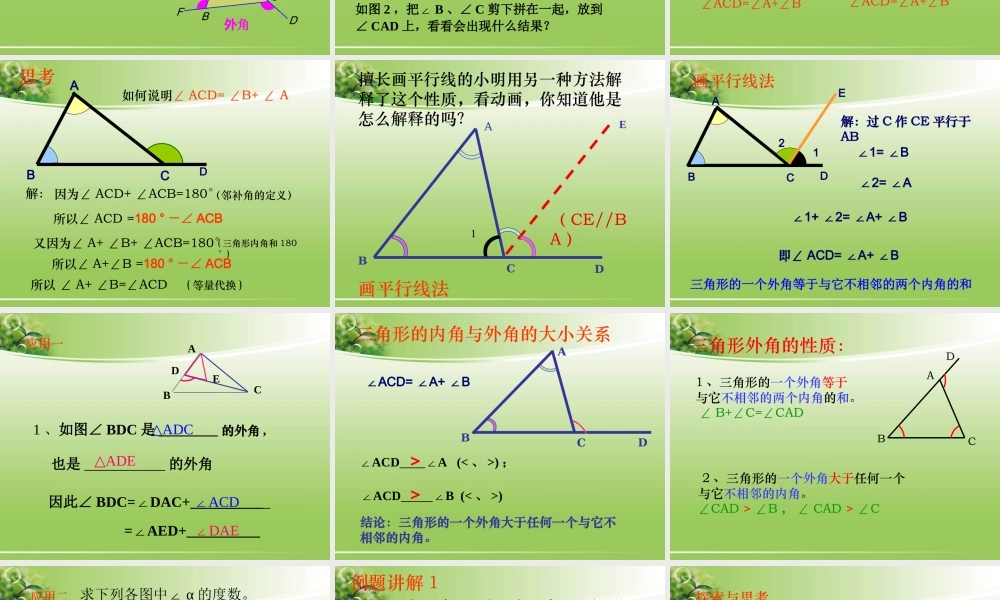
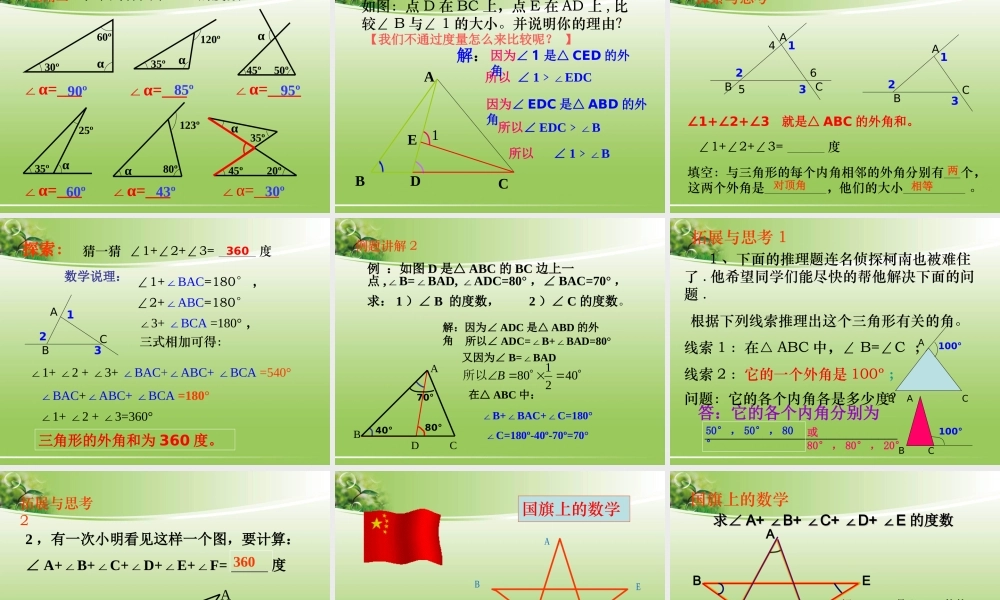
11.2.2 三角形的外角学习目标1 、了解三角形的外角2 、探索并了解三角形的一个外角等于它不相邻的两个内角的和;3 、学会运用简单的说理来计算三角形相关的角重点:三角形的外角性质难点:运用三角形外角性质进行有关计算时能准确地表达推理的过程和方法。重点和难点三角形的内角和等于 180°三角形的内角和定理BAC∠A+∠B+∠C=180°DBAC不相邻内角1234想一想:外角与相邻内角有什么特殊关系?外角∠4+∠3=180°外角与相邻内角的大小不能确定。三角形的一边与另一边的延长线组成的角 , 叫做三角形的外角 .归纳:1 、每一个三角形都有6个外角.3 、每个外角与相应的内角是邻补角.2 、每一个顶点相对应的外角都有2个.相邻内角观察与思考ABDEFC外角ABDEFC外角987654321BCA画一个三角形将它的所有外角画出来。找出三角形的外角在图 1 中,∠ CBD 是△ ABC 的外角,则 ∠ CBD+∠ABC= ( )ABCD图 1180º动动小手 : 在一张白纸上任意画一个三角形 ABC ,如图 2 ,把∠ B 、∠ C 剪下拼在一起,放到∠ CAD 上,看看会出现什么结果?ABCD图 2想一想根据图形计算∠ ACD 的大小 , 通过计算 , 你发现了什么规律?BCAD 350700BA C D 80040075°105°∠ACD=∠A+∠B60°120°∠ACD=∠A+∠BD因为∠ ACD+ ∠ACB=180°又因为∠ A+ ∠B+ ∠ACB=180°所以 ∠ A+ ∠B=∠ACD 解:ABC所以∠ ACD =180 ° -∠ ACB所以∠ A+∠B =180 ° -∠ ACB(邻补角的定义)( 三角形内角和 180 °)( 等量代换 )如何说明∠ ACD= ∠B+ ∠ A思考1( CE//BA )AE擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?CBD画平行线法D解:过 C 作 CE 平行于ABABC12∠1= B∠∠2= A∠∠1+ 2= A+ B∠∠∠即∠ ACD= A+ B∠∠E三角形的一个外角等于与它不相邻的两个内角的和画平行线法∠ACD也是 ___________ 的外角ABCDE因此∠ BDC=DAC+__________∠ △ADE△ADC∠DAE1 、如图∠ BDC 是 ________ 的外角 , =AED+__________∠应用一 ∠ACD A (<∠、 >) ;∠ACD B (<∠、 >)结论:三角形的一个外角大于任何一个与它不相邻的内角。DACB>>∠ACD= ∠A+ ∠B三角形的内角与外角的大小关系ABCD1 、三角形的一个外角等于与它不相邻的两个内角的和。 ∠ B+∠C=∠CAD 2 、三角形的一个外角大于任何一个与它不相邻的内角。 ∠CAD > ∠B , ∠ CAD >...