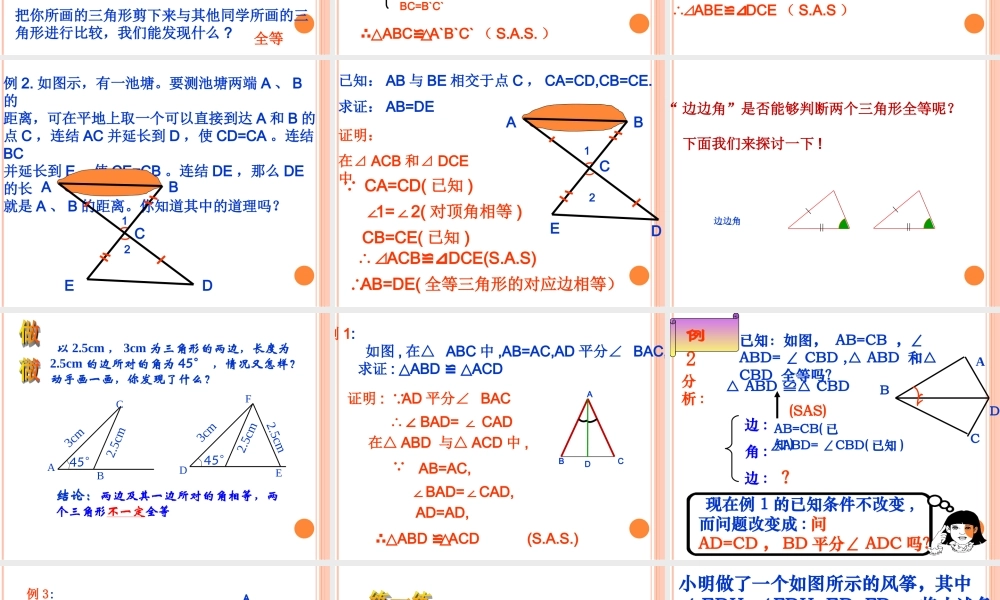
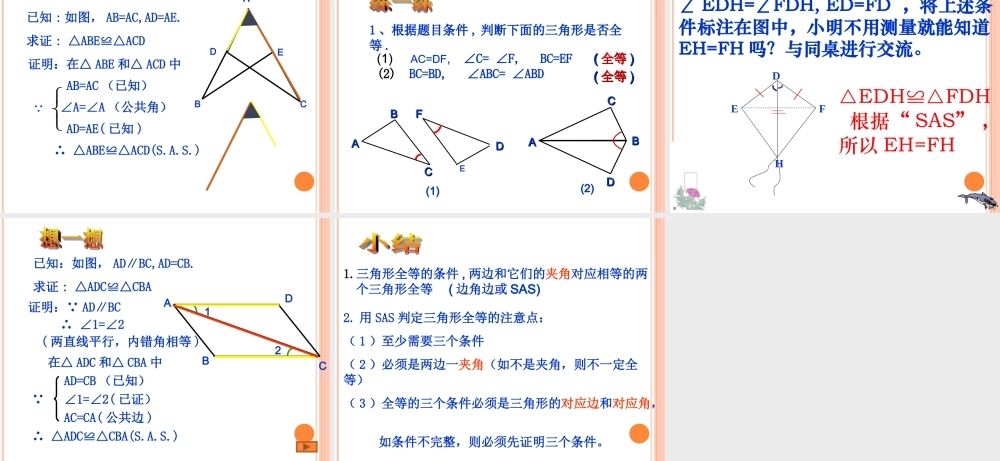
13.2. 三角形全等的判定 3 、边角边 (SAS) 儋州市第二中学 符力探讨 : 如果两个三角形有三组对应相等的元素,那么会有几种可能的情况?1.1. 两边一角对应相等两边一角对应相等 2.2. 两角一边对应相等两角一边对应相等3.3. 三角对应相等三角对应相等4.4. 三边对应相等三边对应相等两边一角又会有哪几种情况?请同学们探讨一下!( 2 )边边角( 1 )边角边夹角“ 边角边”是否能够判断两个三角形全等呢?下面我们来探讨一下 !边角边夹角 如图,已知两条线段和一个角,已这两条线段为边,以这个角为这两条边的夹角,画一个三角形。2.5cm3cm画法: 1. 画∠ MAN= 45°2. 在射线 AM 上截取 AB= 3cm3. 在射线 AN 上截取AC=2.5cm4. 连接 BC∴△ABC 就是所求的三角形把你所画的三角形剪下来与其他同学所画的三角形进行比较,我们能发现什么 ?B3cmC2.5cm45 °NAM45 °全等 两边及其夹角分别相等的两个三角形全等 . 简记 S.A.S.( 或边角边 )结论 : 三角形全等判定方法三角形全等判定方法用符号语言表达为:在△ ABC 与△ A`B`C` 中AB=A`B`∠B=B`∠BC=B`C`∴△ABCA`B`C`≌△( S.A.S. )A′ABCB′C′ 基本事实:例 1. 如图示,已知线段 AC 、 BD 相交于点E , AE=DE,BE=CE. 求证:⊿ ABE ≌⊿DCE.ADBCE证明:在⊿ ABE 和⊿ DCE 中, AE=DE (已知) ∠AEB=DEC(∠对顶角相等 )BE=CE( 已知 )∴⊿ABE ≌⊿DCE ( S.A.S )例 2. 如图示,有一池塘。要测池塘两端 A 、 B的距离,可在平地上取一个可以直接到达 A 和 B 的点 C ,连结 AC 并延长到 D ,使 CD=CA 。连结BC并延长到 E ,使 CE=CB 。连结 DE ,那么 DE的长就是 A 、 B 的距离。你知道其中的道理吗?ABCDE12已知: AB 与 BE 相交于点 C , CA=CD,CB=CE.ABCDE12求证: AB=DE证明:在⊿ ACB 和⊿ DCE中 CA=CD( 已知 )∠1=2(∠对顶角相等 )CB=CE( 已知 ) ∴ ⊿ACBDCE(S.A.S)≌⊿∴AB=DE( 全等三角形的对应边相等)“ 边边角”是否能够判断两个三角形全等呢? 下面我们来探讨一下 !边边角 以 2.5cm , 3cm 为三角形的两边,长度为2.5cm 的边所对的角为 45° ,情况又怎样?动手画一画,你发现了什么?ABCDEF2.5cm3cm45°45°3cm结论:两边及其一边所对的角相等,两个三角形不一定全等2.5cm2.5cm例 1: 如图 , 在△ ABC 中 ,AB=AC,AD 平分∠ B...