正弦定理约课时VIP免费

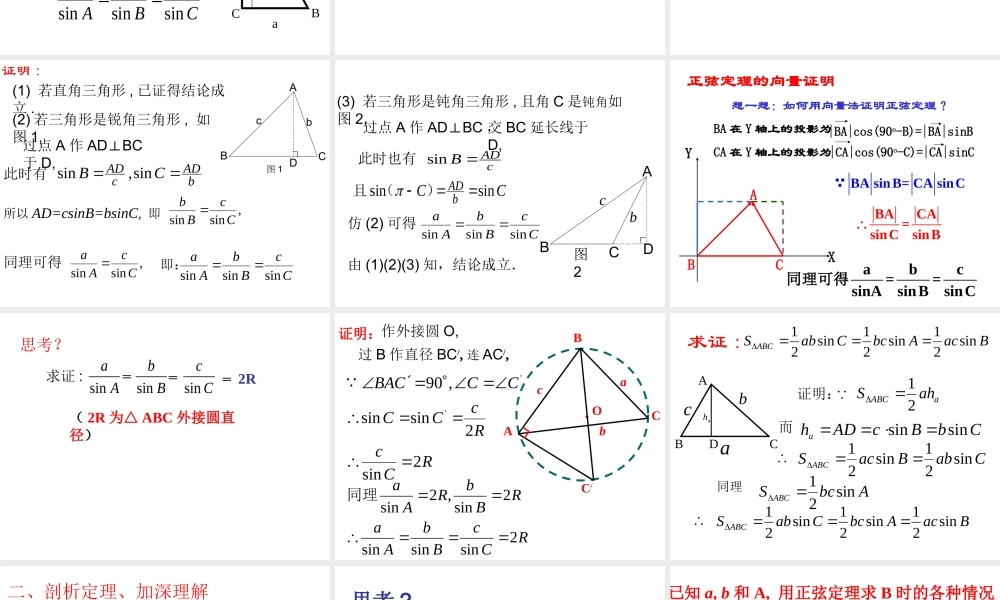
主备人：罗瑜 唐强 审核人：牟必继1.1.1 正弦定理 善于奋飞的人天上有路，敢于攀登的人山中有路，勇于远航的人海里有路，勤于学习的人脚下有路 ! .(1) 在我国古代就有嫦娥奔月的神话故事 . 明月 高悬 , 我们仰望夜空 , 会有无限遐想 , 不禁会问 , 月亮离我们地球有多远呢 ? 科学家们是怎样 测出来的呢？问题的引入： (2) 设 A,B 两点在河的两岸 , 只给你米尺和量角设备 , 不过河你可以测出它们之间的距离吗 ?AB我们这一节所学习的内容就是解决这些问题的有力工具 . ABC3C2C1CBC 的长度与角 A 的大小有关吗 ?三角形中角 A 与它的对边 BC 的长度是否存在定量关系 ?1.1.1 正弦定理 在 RtABC△中 , 各角与其对边的关系 :caA sincbB sin1sinC不难得到 :CcBbAasinsinsinCBAabc cc 在非直角三角形 ABC 中有这样的关系吗 ?AcbaCB 一、正弦定理 : 在一个三角形中 , 各边和它所对角的正弦的比相等 .CcBbAasinsinsin即 (1) 若直角三角形 , 已证得结论成立 .bADcADCBsin,sin所以 AD=csinB=bsinC, 即,sinsinCcBb同理可得,sinsinCcAaCcBbAasinsinsin即：DAcbCB图 1过点 A 作 ADBC⊥于 D,此时有 证明 :(2) 若三角形是锐角三角形 , 如图 1, 由 (1)(2)(3) 知，结论成立．CCbADsinsin）（且CcBbAasinsinsin仿 (2) 可得D(3) 若三角形是钝角三角形 , 且角 C 是钝角如图 2, 此时也有cADB sin交 BC 延长线于D,过点 A 作 ADBC⊥，CAcbB图2 YX正弦定理的向量证明BAC想一想：如何用向量法证明正弦定理？BA 在 Y 轴上的投影为CA 在 Y 轴上的投影为BA sinB= CA sinC�BACA=sinCsinBabc==sinAsinBsinC同理可得|BA|cos(90o-B)=|BA|sinB|CA|cos(90o-C)=|CA|sinC AasinBbsinCcsin＝＝（ 2R 为△ ABC 外接圆直径）＝ 2R思考？求证 : 证明：OC/cbaCBARCcRcCCCCCBA2sin2sinsin,90''RCcBbAaRBbRAa2sinsinsin2sin,2sin同理作外接圆 O,过 B 作直径 BC/, 连 AC/, 证明： BacAbcCabS ABCsin21sin21sin21BACDabcaABCahS21而CbBcADhasinsin∴CabBacS ABCsin21sin21同理∴BacAbcCabS ABCsin21sin21sin21haAbcS ABCsin21求证 : 二、剖析定理、加深理解正弦定理可以解决三角形中哪类问题： ①已知两角和一边，求其他角和边 ...