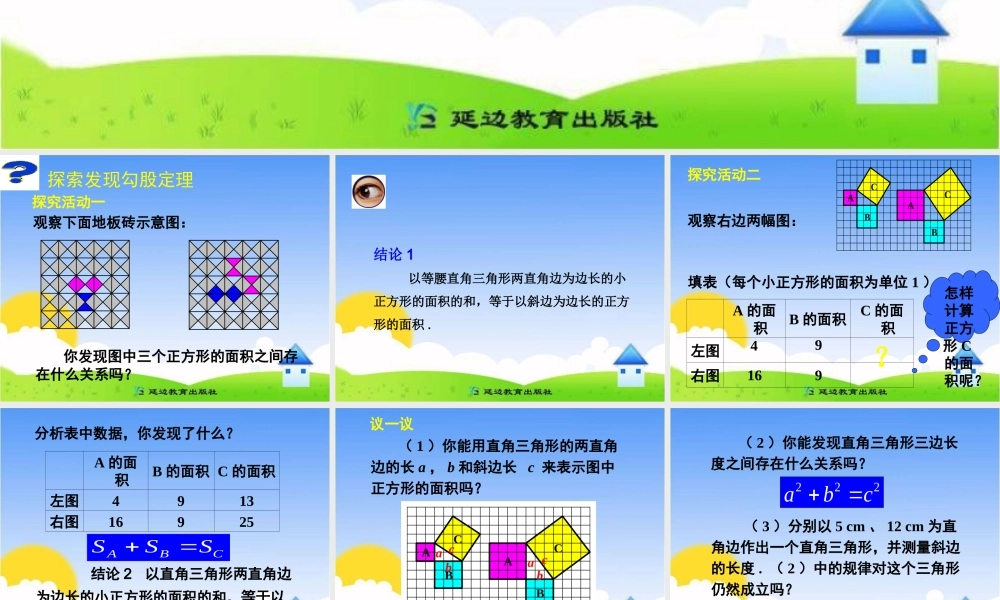
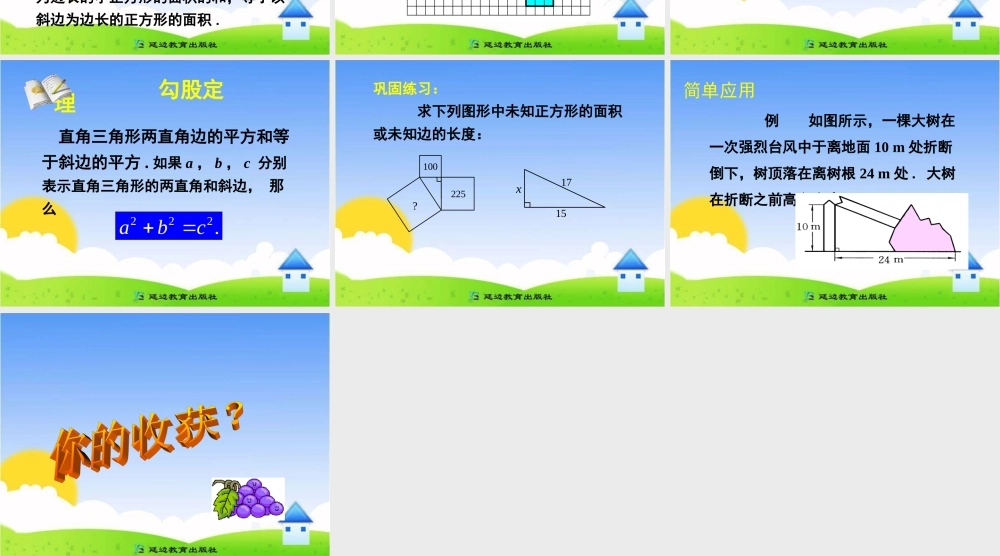
第一章 勾股定理1. 探索勾股定理(第 1 课时)探究活动一 观察下面地板砖示意图:探索发现勾股定理 你发现图中三个正方形的面积之间存在什么关系吗?结论 1 以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积 .探究活动二ABCCBA观察右边两幅图: 填表(每个小正方形的面积为单位 1 )A 的面积B 的面积C 的面积左图右图4 ?怎样计算正方形 C的面积呢?9 16 9 分析表中数据,你发现了什么? A 的面积B 的面积 C 的面积左图4913右图16925ABCSSS 结论 2 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积 .议一议 ( 1 )你能用直角三角形的两直角边的长 a , b 和斜边长 c 来表示图中正方形的面积吗? ABCCBA abcabc ( 2 )你能发现直角三角形三边长度之间存在什么关系吗?222abc ( 3 )分别以 5 cm 、 12 cm 为直角边作出一个直角三角形,并测量斜边的长度 . ( 2 )中的规律对这个三角形仍然成立吗? 直角三角形两直角边的平方和等于斜边的平方 . 如果 a , b , c 分别表示直角三角形的两直角和斜边, 那么222.abc 勾股定理 222.abc巩固练习: 求下列图形中未知正方形的面积或未知边的长度: ?225100x1517简单应用 例 如图所示,一棵大树在一次强烈台风中于离地面 10 m 处折断倒下,树顶落在离树根 24 m 处 . 大树在折断之前高多少米?