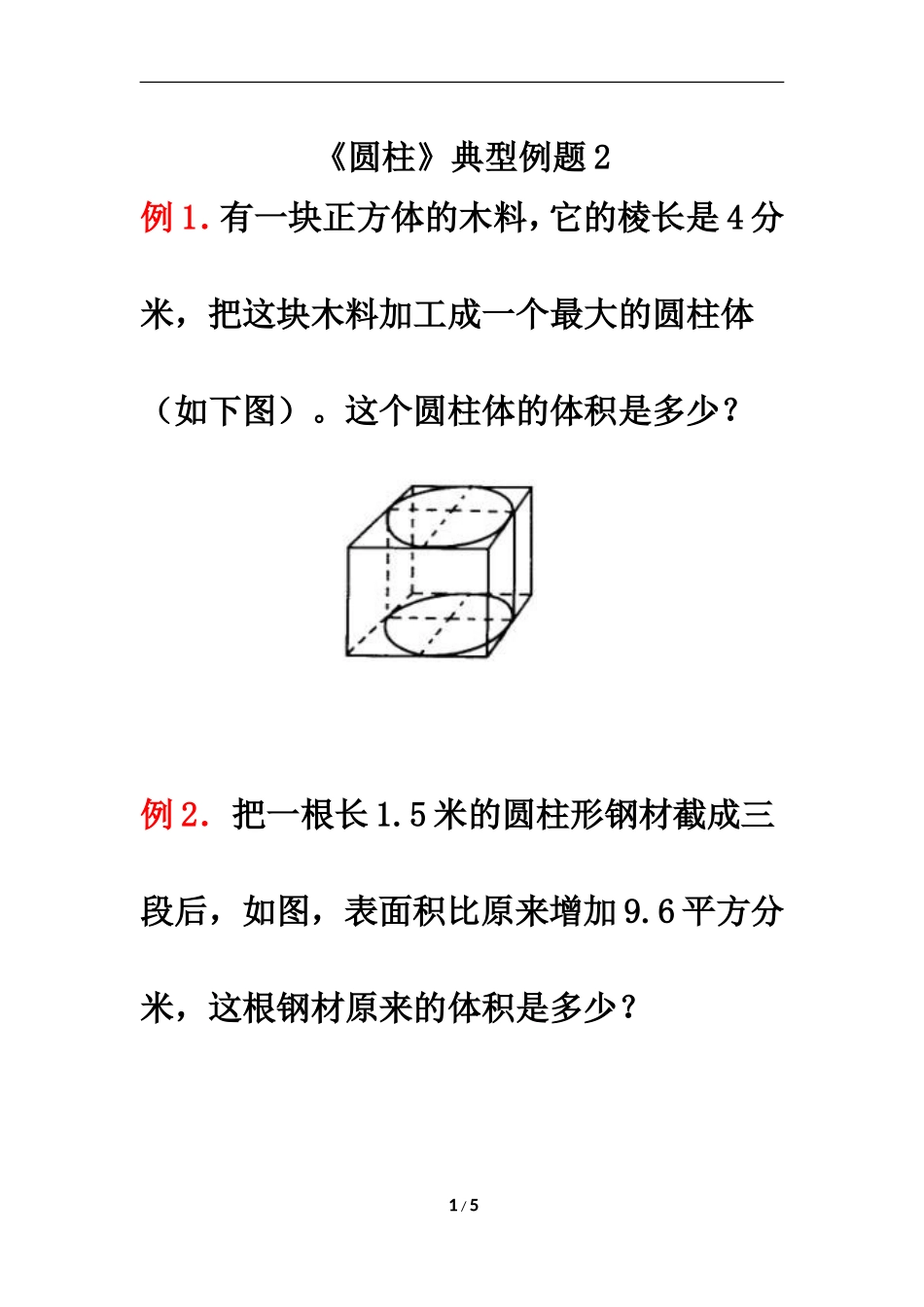
《圆柱》典型例题 2例 1.有一块正方体的木料,它的棱长是 4 分米,把这块木料加工成一个最大的圆柱体(如下图)。这个圆柱体的体积是多少?例 2.把一根长 1.5 米的圆柱形钢材截成三段后,如图,表面积比原来增加 9.6 平方分米,这根钢材原来的体积是多少? 1 / 5例 3.一个圆柱体的高是 37.68 厘米,它的侧面展开后恰好是正方形,这个圆柱体的体积是多少立方厘米?(保留整数)例 4.一个圆柱体水桶,从里面量,底面直径是 32 厘米,高是 50 厘米.这个水桶大约能盛水多少千克?(1 立方分米的水重 1 千克) 2 / 5例 5.一个圆柱量桶,底面半径是 5 厘米,把一块铁块从这个量桶里取出后,水面下降 3厘米,这块铁块的体积是多少? 参考答案 3 / 5例 1 分析:由圆柱体的体积公式可知:圆柱体的体积大小的决定因素是底面半径和高。因此,要想使加工成的圆柱体的体积最大,则必须满足圆柱底面的直径等于正方体的棱长,高也等于正方体的棱长。 解:3.14×(4÷2)×(4÷2)×4=50.24(立方分米) 答:这个圆柱体的体积是 50.24 立方分米。例 2 分析:从图中观察,可将这段钢材截成三段,表面积增加四个与圆柱底面完全相等的圆面积,因此就可以求出圆柱形钢材的底面积,长 1.5 米就是圆柱的高于是问题得到解决。 解: 9.6÷4×15←注意统一单位 =2.4×15 =36(立方分米) 答:这根钢材原来体积是 36 立方分米。例 3 分析:“它的侧面展开后恰好是正方形,”通过这个条件可以想象出圆柱的高就是正方形的边长,也是圆柱的底面周长,这样转化后,问题也就得到解决。 解:1.半径:37.68÷3.14÷2=6(厘米) 2.体积:3.14×6×6×37.68=4259.3472≈4259(立方厘米) 答:这个圆柱体的体积约是 4259 立方厘米。例 4 分析:圆柱形水桶的底面积是: (平方厘米) 圆柱形水桶的容积是 803.84×50=40192(立方厘米), 折合成立方分米数是 40192÷1000=40.192(立方分米), 大约能盛水的重量是 1×40.192≈40(千克) 答:这个水桶大约能盛水 40 千克。 4 / 5例 5 分析:认真读题后,找出题中关键句或词进行分析思考,这是解决问题的重要方法,“把一块铁块从这个量桶里取出后,水面下降 3 厘米”通过这个变化可以想象出,原来铁块的体积就是水面下降 3 厘米这个高度的体积,这是铁块原来占的空间,于是问题得到解决。 解:5×5×3.14×3=235.5(立方厘米) 答:这块铁块的体积是 235.5 立方厘米。 5 / 5