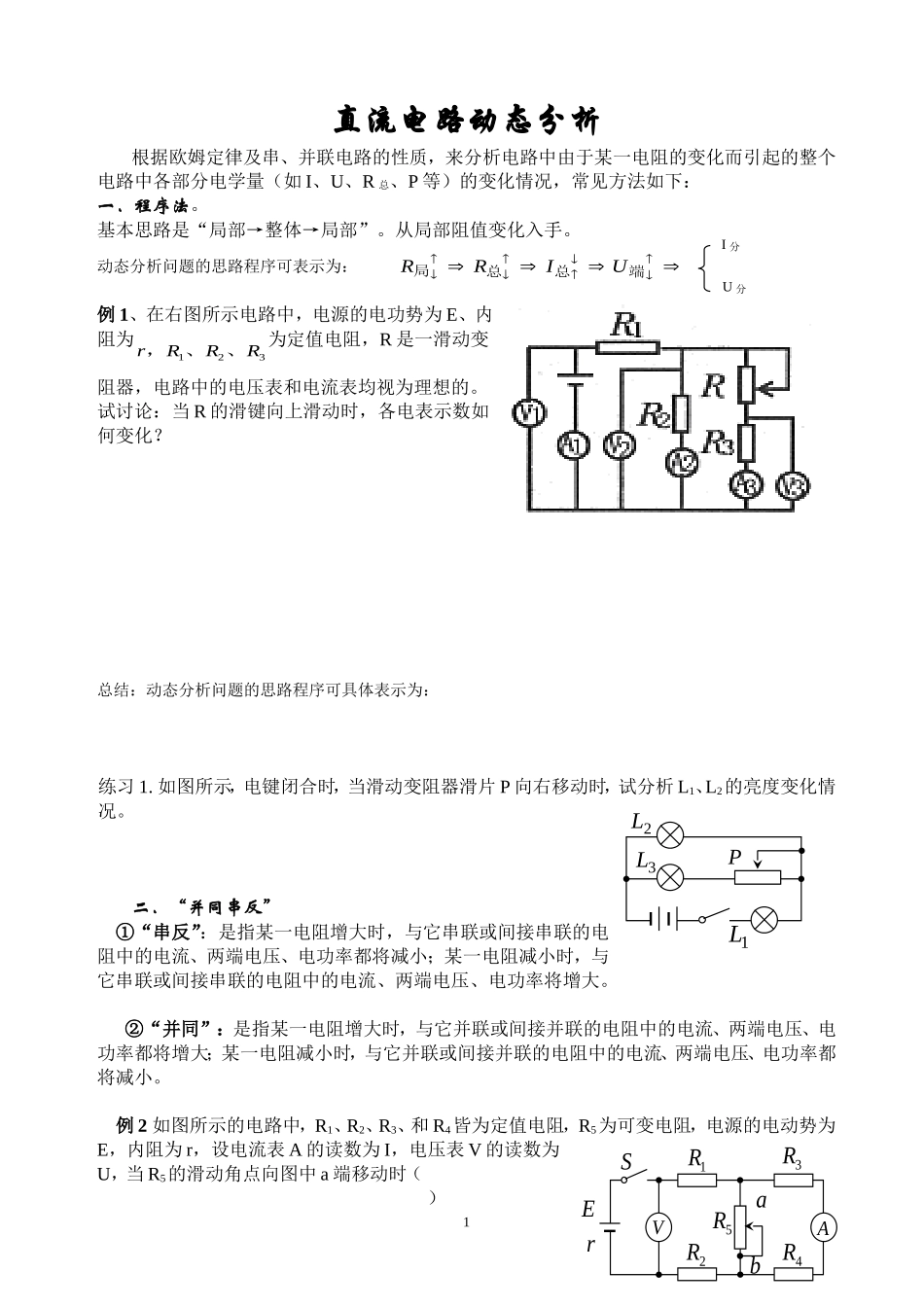
直流电路动态分析根据欧姆定律及串、并联电路的性质,来分析电路中由于某一电阻的变化而引起的整个电路中各部分电学量(如 I、U、R 总、P 等)的变化情况,常见方法如下:一.程序法。基本思路是“局部→整体→局部”。从局部阻值变化入手。动态分析问题的思路程序可表示为: 例 1、在右图所示电路中,电源的电功势为 E、内阻为rRRR,、、123 为定值电阻,R 是一滑动变阻器,电路中的电压表和电流表均视为理想的。试讨论:当 R 的滑键向上滑动时,各电表示数如何变化? 总结:动态分析问题的思路程序可具体表示为:练习 1. 如图所示,电键闭合时,当滑动变阻器滑片 P 向右移动时,试分析 L1、L2的亮度变化情况。二.“并同串反”①“串反”:是指某一电阻增大时,与它串联或间接串联的电阻中的电流、两端电压、电功率都将减小;某一电阻减小时,与它串联或间接串联的电阻中的电流、两端电压、电功率将增大。 ②“并同”:是指某一电阻增大时,与它并联或间接并联的电阻中的电流、两端电压、电功率都将增大;某一电阻减小时,与它并联或间接并联的电阻中的电流、两端电压、电功率都将减小。例 2 如图所示的电路中,R1、R2、R3、和 R4皆为定值电阻,R5为可变电阻,电源的电动势为E,内阻为 r,设电流表 A 的读数为 I,电压表 V 的读数为U,当 R5的滑动角点向图中 a 端移动时()1端总总局UIRRI 分U 分VA1R2R3R4R5RErSab1L2LP3LA.I 变大,U 变小B、I 变大,U 变大C、I 变小,U 变大D、I 变小,U 变小注意“串反并同”法则的应用条件:单变量电路。对于多变量引起的电路变化,若各变量对同一对象分别引起的效果相同,则该原则的结果成立;若各变量对同一对象分别引起的效果相反,则“串反并同”法则不适用。例2、如图(1)所示电路中,闭合电键 S,当滑片 P 向右移动时,灯泡 L1、L2的亮度变化如何?分析与解:本题中滑动变阻器左右两部分都接入电路,等效电路如图(2)所示,变阻器 R分解得到两变量 R1、R2,由图可知:滑片 P 向右移 → R1( ),R2( )对灯泡 L1: 对灯泡 L2: 三.特殊值法与极限法:① 极限法:即因滑动变阻器滑片滑动引起电路变化的问题,可将变阻器的滑动端分别滑至两个极端去讨论。特殊值法:对于某些双臂环路问题,可以采取代入特殊值去判定,从而找出结论例 3:在输液时,摇曳有时会从针口流出体外,为了及时发现,设计了一种报警装置,...