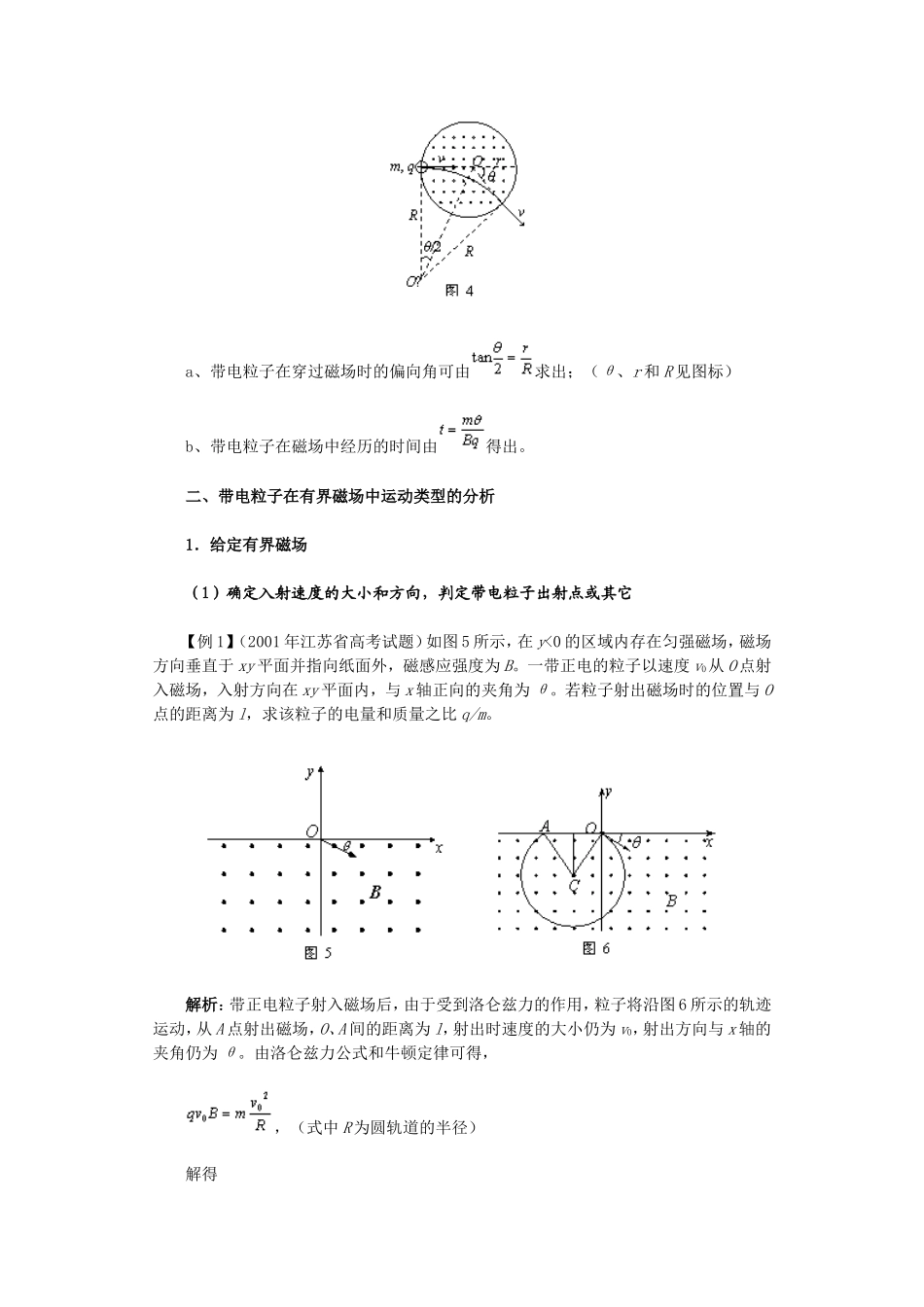
带电粒子在有界磁场中运动的临界问题 当某种物理现象变化为另一种物理现象或物体从一种状态变化为另一种状态时,发生这种质的飞跃的转折状态通常称为临界状态。粒子进入有边界的磁场,由于边界条件的不同,而出现涉及临界状态的临界问题,如带电粒子恰好不能从某个边界射出磁场,可以根据边界条件确定粒子的轨迹、半径、在磁场中的运动时间等。如何分析这类相关的问题是本文所讨论的内容。 一、带电粒子在有界磁场中运动的分析方法 1.圆心的确定 因为洛伦兹力 F 指向圆心,根据 F⊥v,画出粒子运动轨迹中任意两点(一般是射入和射出磁场两点),先作出切线找出 v 的方向再确定 F 的方向,沿两个洛伦兹力 F 的方向画其延长线,两延长线的交点即为圆心,或利用圆心位置必定在圆中一根弦的中垂线上,作出圆心位置,如图 1 所示。 2.半径的确定和计算 利用平面几何关系,求出该圆的可能半径(或圆心角),并注意以下两个重要的几何特点: ①粒子速度的偏向角 φ 等于转过的圆心角 α,并等于 AB 弦与切线的夹角(弦切角)θ 的 2 倍,如图 2 所示,即 φ=α=2θ。 ②相对的弦切角 θ 相等,与相邻的弦切角 θ′互补,即 θ+θ′=180°。 3.粒子在磁场中运动时间的确定 若要计算转过任一段圆弧所用的时间,则必须确定粒子转过的圆弧所对的圆心角,利用圆心角 α 与弦切角的关系,或者利用四边形内角和等于 360°计算出圆心角 α 的大小,并由表达式,确定通过该段圆弧所用的时间,其中 T 即为该粒子做圆周运动的周期,转过的圆心角越大,所用时间 t 越长,注意 t 与运动轨迹的长短无关。 4.带电粒子在两种典型有界磁场中运动情况的分析 ①穿过矩形磁场区:如图 3 所示,一定要先画好辅助线(半径、速度及延长线)。 a、带电粒子在穿过磁场时的偏向角由 sinθ=L/R 求出;(θ、L 和 R 见图标) b、带电粒子的侧移由 R2=L2-(R-y)2解出;(y 见所图标) c、带电粒子在磁场中经历的时间由得出。 ②穿过圆形磁场区:如图 4 所示,画好辅助线(半径、速度、轨迹圆的圆心、连心线)。 a、带电粒子在穿过磁场时的偏向角可由求出;(θ、r 和 R 见图标) b、带电粒子在磁场中经历的时间由得出。 二、带电粒子在有界磁场中运动类型的分析 1.给定有界磁场 (1)确定入射速度的大小和方向,判定带电粒子出射点或其它 【例 1】(2001 年江苏省高考试题)如图 5 所示,在 y<0 ...