定积分的简单几何应用VIP免费

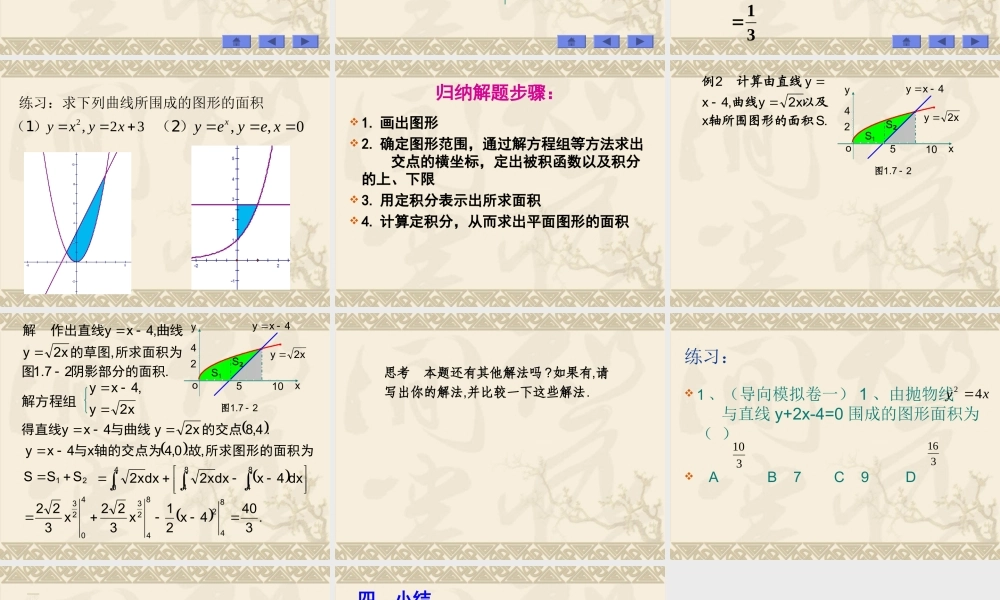
§1.7 §1.7 定积分的简单应用定积分的简单应用 §1.7.1 §1.7.1 定积分的几何应用 1. 定积分的几何意义badxxfS )(图 10bxy x f y)(a 如果在区间 [a,b] 上函数 f(x) 连续且恒有 f(x) ≥0, 那么定积分 表示由直线 x=a,x=b.y=0 和曲线 所围成的曲边梯形的面积。dxxfba)(A=0)(xf0)(xfA 表示以 y=f(X) 为曲边的曲边梯形面积aby=f(x)>0xy0Ay=f(x)<0abxy0Adxxfba)(3. 定积分的综合应用图 10bxy xg y)( x f y)(ababadxxgdxxfS )()(badxxgxfs )]()([例 23xy x20y1解 所围成的图形如图所示：3xy 求2 ,1xx与直线轴所围成的及 x平面图形的面。20 30 1 3dxxdxxs417则例 222y, xxy计算与两条抛物线 的面积所围成的图形解 作出两条曲线的草图，所围成的图形如图中阴影部分所示 : 2xy 2yx 110yx解方程组 22yxxy线的交点坐标为 得两抛物)0 ,0(),1 ,1(和则图形的面积为1 0 2 ][dxxxS3110223332xx2xy 2yx 110yx2,23yxyx练习：求下列曲线所围成的图形的面积（1）,,0xyeye x（2）归纳解题步骤： 1. 画出图形 2. 确定图形范围，通过解方程组等方法求出 交点的横坐标，定出被积函数以及积分的上、下限 3. 用定积分表示出所求面积 4. 计算定积分，从而求出平面图形的面积.Sxx2y,4xy2轴所围图形的面积以及曲线计算由直线例oxy510244xyx2y 27.1图1S2S.27.1,x2y,4xy阴影部分的面积图所求面积为的草图曲线作出直线解解方程组x2y,4xy.4,8x2y4xy的交点与曲线得直线所求图形的面积为故的交点为轴与,.0,4x4xy21SSS848440dx4xdxx2dxx2.3404x21x322x32284284234023oxy510244xyx2y 27.1图1S2S.,,?并比较一下这些解法写出你的解法请如果有本题还有其他解法吗思考练习： 1 、（导向模拟卷一） 1 、由抛物线 与直线 y+2x-4=0 围成的图形面积为（ ） A B 7 C 9 D 310316xy42 ( 第四次模拟 9) 如图，由曲线 (x>0) ，直线 x=1 及 y=x-2 围成的区域为 D ，往该区域内投一点 P ，则点 P 落在 内的概率是 （ ） A B. C D . xy3ABC213ln613ln23ln311. 定积分的几何意义2. 用定积分求曲边梯形面积的结题步骤 四、小结