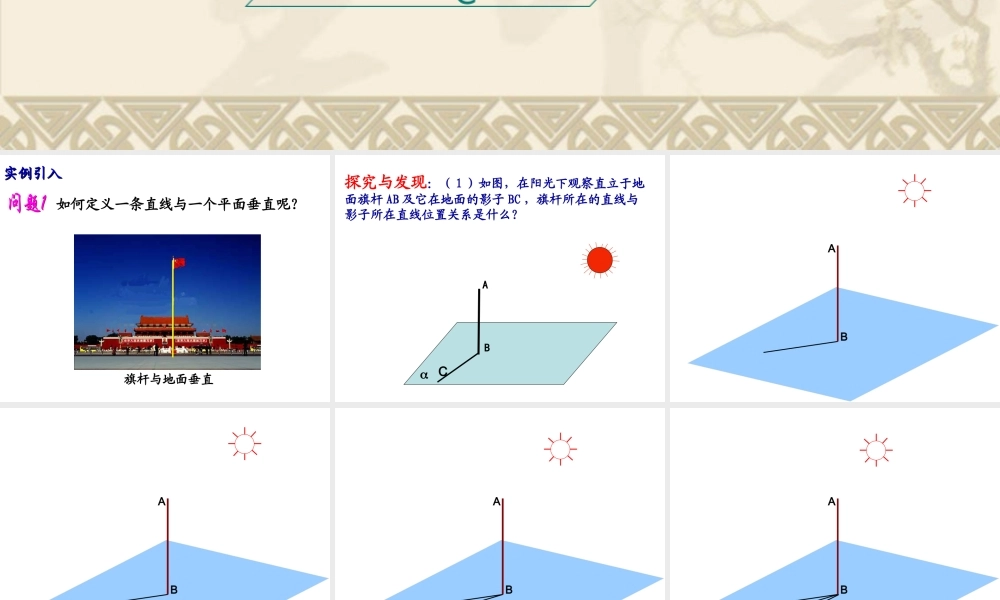
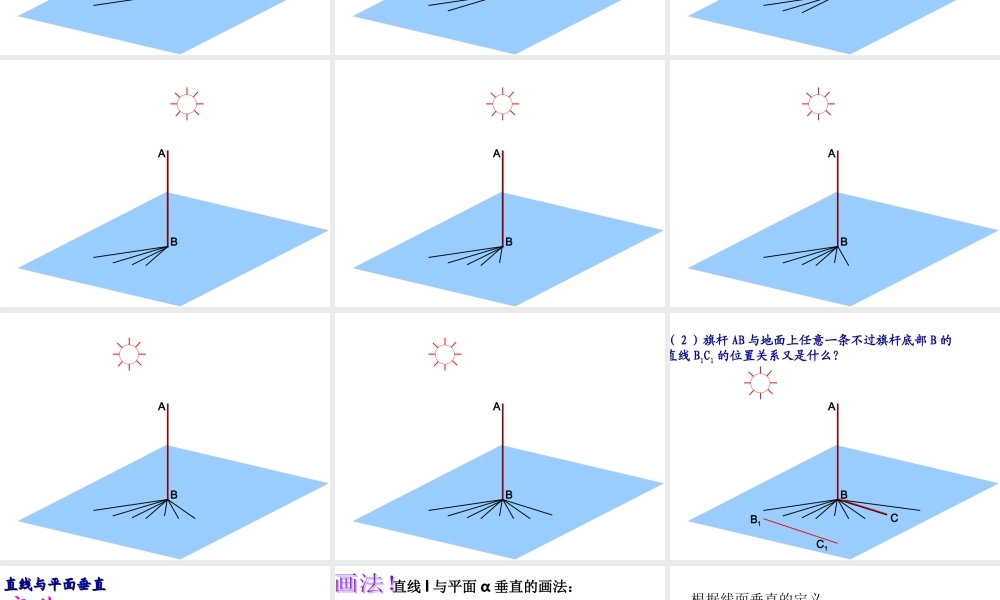
ABCDα 实例引入实例引入旗杆与地面垂直如何定义一条直线与一个平面垂直呢? AB探究与发现:( 1 )如图,在阳光下观察直立于地面旗杆 AB 及它在地面的影子 BC ,旗杆所在的直线与影子所在直线位置关系是什么?C AB AB AB AB AB AB AB AB AB CC1B1AB( 2 )旗杆 AB 与地面上任意一条不过旗杆底部 B 的直线 B1C1 的位置关系又是什么? lP 如果直线 l 与平面 内的任意一条直线都垂直,我们说直线 l 与平面 互相垂直,记作 .l平面 的垂线直线 l 的垂面垂足直线与平面垂直直线与平面垂直返回 直线 l 与平面 α 垂直的画法:通常把直线画成与表示平面的平行四边形的一边垂直。 aαb 结论: 如果一条直线垂直一个平面,那么这条直线就垂直于这个平面内的任意一条直线。ab符号语言:ab线面垂直,则线线垂直简记为: 根据线面垂直的定义 α下列命题是否正确,为什么(举例说明)?( 1 )如果平面外一条直线垂直于一个平面内的无数条直线,那么这条直线与这个平面垂直。辨析( 2 )如果一条直线垂直一个平面,那么这条直线就垂直于这个平面内的任一直线。aαb定义CBA α A1B1D1C1BDCAB1D1C1A1ABCDA1B1D1C1ABCD实验:如下图,请同学们准备一块三角形的纸片。BDCA过 ABC 的顶点 A 翻折纸片,得到折痕 AD ,将翻折后的纸片竖起放置在桌面上( BD , DC 与桌面接触)。 ( 1 )折痕 AD 与桌面垂直吗? ( 2 )如何翻折才能使折痕与桌面所在的平面 α 垂直?思考:我们如何证明直线与平面垂直 ?是否一定要证明直线与平面中的所有直线垂直 ?AD 作为 BC 边上的高时 ,AD α ,这时 AD BC, 即 AD BD , AD CD , BD∩CD=D.结论: AD⊥BD , AD⊥CD , BD∩CD=D ,有 AD⊥α. 判定定理判定定理 :: 一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.balA作用:判定直线与平面垂直的依据.直线与平面垂直直线与直线垂直思想:直线与平面垂直直线与平面垂直判定定理判定定理lalbababAl符号语言: 直线与平面垂直直线与平面垂直判定定理解读判定定理解读( 1 )简记为:( 2 ) 5 个条件缺一不可线线垂直 线面垂直其中关键在于一条直线垂直于平面内的两条相交直线 例 1 如图,已知 ,求证aba,//.bbamn根据直线与平面垂直的定义知.,nama又 ab//∴.,nbmb∴.b...