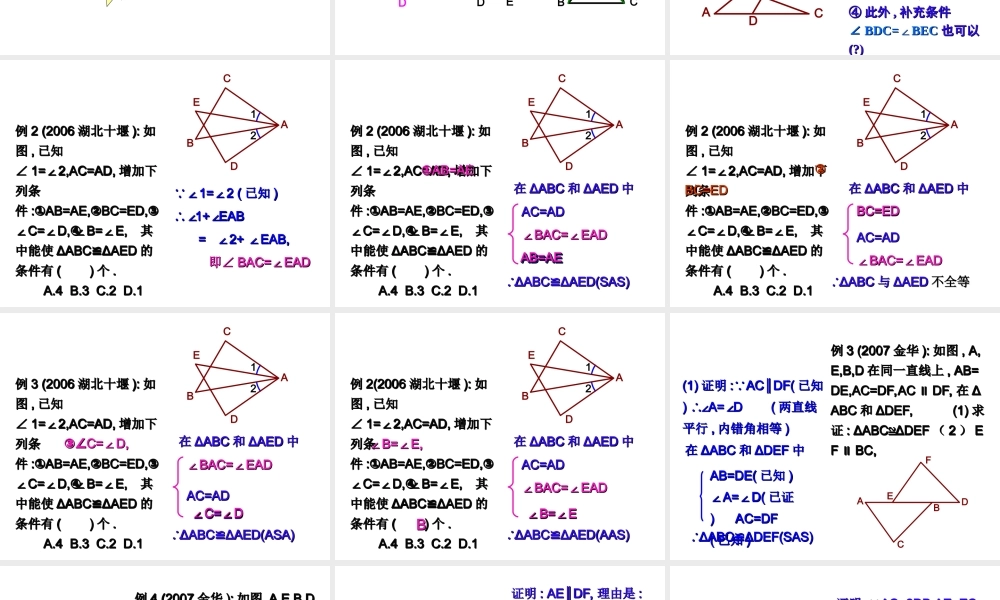
11.2 全等三角形复习甘南三中八年级数学组 1 、判定 1 :三边对应相等的两个三角形全等。简称“边边边”( SSS )2 、判定 2 :两边和它们的夹角对应相等的两个三角形全等。简称“边角边”( SAS )。一、复习全等三角形的判定 3 、判定 3 :两角和它们的夹边对应相等的两个三角形全等。简称“角边角”( ASA )4 、判定 4 :两角和其中一角的对边对应相等的两个三角形全等。简称“角角边”( AAS )5 、判定 5 :斜边和一直角边对应相等的两个直角三角形全等。简称“斜边 , 直角边”( HL ) 二、几种常见全等三角形基本图形二、几种常见全等三角形基本图形FEDCBAFEDCBAFEDCBA平移 EDCBAEDCBA旋转 EDCBADCBADCBAEDCBAOEDCBA翻折 例例 1 (20061 (2006 湖南株洲湖南株洲 ):):如图如图 ,AE=AD,,AE=AD, 要使要使ΔABDΔACE,≌ΔABDΔACE,≌请你增请你增加一个条件是加一个条件是 ..EDCBA分析分析 :: 现在我们已知 现在我们已知 SS→ AE=AD→ AE=AD①① 用用 SAS,SAS, 需要补充条需要补充条件件 AB=AC, AB=AC, ②② 用用 ASA,ASA, 需要补充条需要补充条件件∠∠ ADB=AEC, ∠ADB=AEC, ∠ ③③ 用用 AAS,AAS, 需要补充条需要补充条件件∠∠ B= C, ∠B= C, ∠④④ 此外此外 ,, 补充条件补充条件∠∠ BDC=BEC∠BDC=BEC∠也可以也可以(?)(?) SASSASASAASAAASAAS(CD=BE(CD=BE 行吗行吗 ?)?)AA→A=A (∠∠→A=A (∠∠公共公共角角 ) .) .2 、典型例题 例例 2 (20062 (2006 湖北十堰湖北十堰 ):): 如如图图 ,, 已知已知∠∠ 1=2,AC=AD,∠1=2,AC=AD,∠增加下增加下列条列条件件 :AB=AE,BC=ED,①②③:AB=AE,BC=ED,①②③C=D, B=E,∠∠∠∠④C=D, B=E,∠∠∠∠④其其中能使中能使 ΔABCΔAED≌ΔABCΔAED≌的的条件有条件有 ( )( ) 个个 . . A.4 B.3 C.2 D.1 A.4 B.3 C.2 D.121EDCBA ∠ ∠1=2 (∠1=2 (∠已知已知 ) ) 1+ EAB ∴∠∠ 1+ EAB ∴∠∠ = 2+ EAB,∠∠ = 2+ EAB,∠∠ 即∠即∠ BAC=EAD∠BAC=EAD∠ 例例 2 (20062 (2006 湖北十堰湖北十堰 ):): 如如图图 ,, 已知已知∠∠ 1=2,AC=AD,∠1=2,AC=AD,∠增加下增加下列条列条件件 :AB=AE,BC=ED,①②③:AB=AE,BC=ED,①②③C=D, B=E,∠∠∠∠④C=D, B=E,∠∠∠∠④其其中能使中能使 ΔABCΔAED≌ΔABCΔAED≌的的条件有条件有 ( )( ) 个个 . . A.4 B....