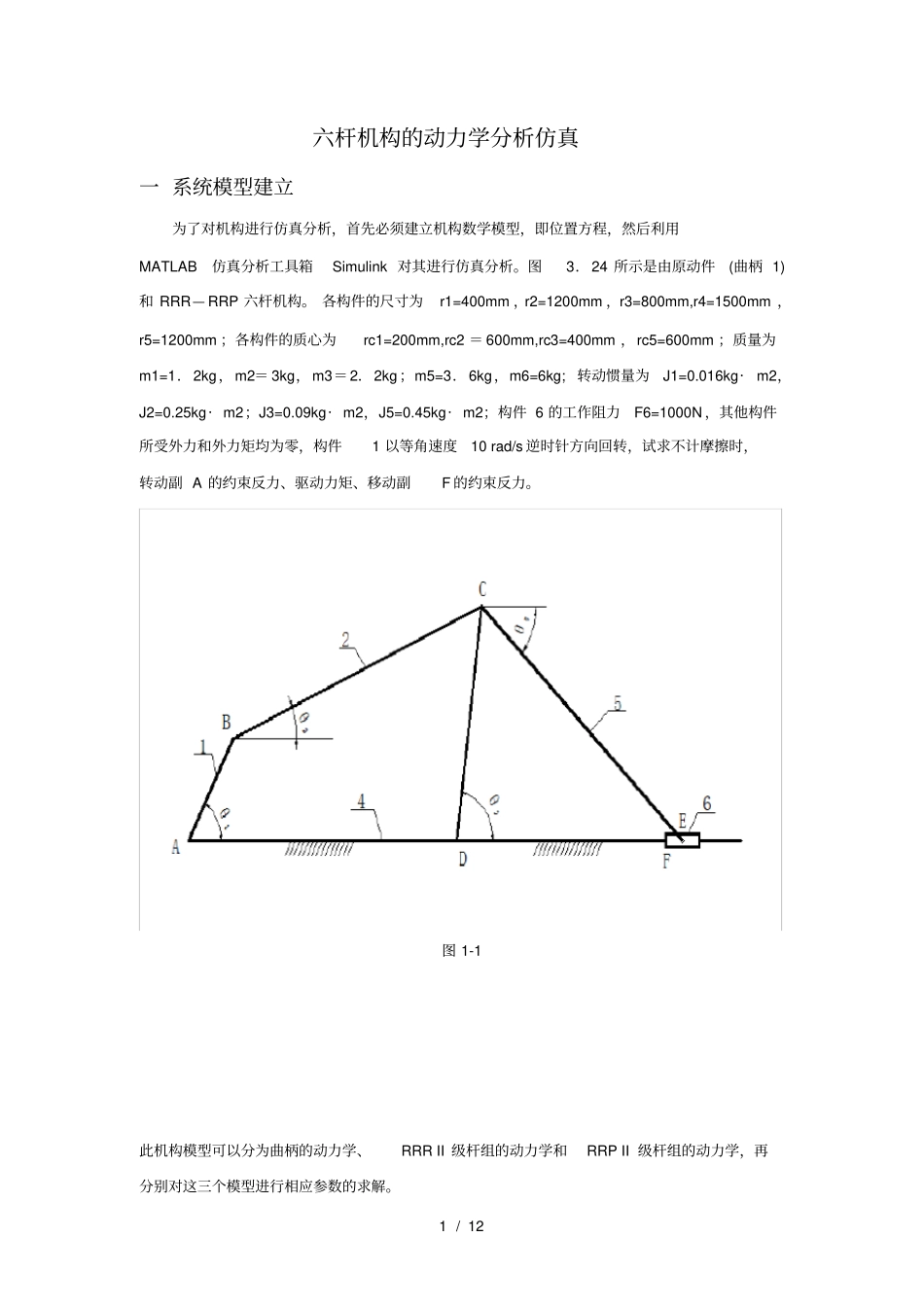
1 / 12 六杆机构的动力学分析仿真一 系统模型建立为了对机构进行仿真分析,首先必须建立机构数学模型,即位置方程,然后利用MATLAB仿真分析工具箱Simulink 对其进行仿真分析。图3.24 所示是由原动件(曲柄 1)和 RRR— RRP 六杆机构。 各构件的尺寸为r1=400mm ,r2=1200mm ,r3=800mm,r4=1500mm ,r5=1200mm ;各构件的质心为rc1=200mm,rc2 = 600mm,rc3=400mm ,rc5=600mm ;质量为m1=1.2kg,m2= 3kg,m3=2.2kg;m5=3.6kg,m6=6kg; 转动惯量为J1=0.016kg·m2,J2=0.25kg· m2;J3=0.09kg· m2,J5=0.45kg· m2;构件 6 的工作阻力F6=1000N ,其他构件所受外力和外力矩均为零,构件1 以等角速度10 rad/s 逆时针方向回转,试求不计摩擦时,转动副 A 的约束反力、驱动力矩、移动副F 的约束反力。图 1-1 此机构模型可以分为曲柄的动力学、RRR II 级杆组的动力学和RRP II 级杆组的动力学,再分别对这三个模型进行相应参数的求解。2 / 12 图 1-2 AB 构件受力模型如上图 1-2 对于曲柄 AB由理论力学可以列出表达式:111XAReR??smFRXXB111y AImR??smFRyyB1111111111111cos)(sin)(cossin??JrrRrrRrRrRMMcyBcXBcyAcXAF由运动学知识可以推得:)cos()2/cos(ReRe12111111???????ccrrAs)sin()2/sin(ImIm12111111???????ccrrAs将上述各式合并成矩阵形式有,??????????gmRFrmrmAmRFrmrmAmMRRyByccXBXccyAXA111211111111112111111111)sin()2/sin(Im)cos()2/cos(Re(1-21) 如图 1-3,对构件 BC 的约束反力推导如下,3 / 12 图 1-3 BC 构件受力模型222Re??smRFRXCXXB2222Im??smgmRFRyCyyB2222222222222cos)(sin)(cossin??JrrRrrRrRrRMcyCcXCcyBcXB如图 1-4,对构件 BC 的约束反力推导如下,图 1-4 CD 构件受力模型333Re??smRFRXCXXD3333Im??smgmRFRyCyyD3333333333333cos)(sin)(cossin??JrrRrrRrRrRMcyCcXCcyDcXD由运动学可以推导得,4 / 12 )sin()2/sin(ImIm22222222???????ccrrBs)cos()2/cos(ReRe22222222???????ccrrBs)cos()2/cos(ReRe32333333???????ccrrDs)sin()2/sin(ImIm32333333???????ccrrDs将上述 BC 构件, CD 构件各式合并成矩阵形式有,33333333332222222222cossincos)(sin)(0010100001010000cos)(sin)(cossin001010000101ccccccccrrrrrrrrrrrryDXDyCXCyBXBRRRRRR=????????????????????????3333332333333333323333333322222222222222222222222222)sin()2/sin(Im)cos()2/cos(...