对数函数及其性质一VIP免费

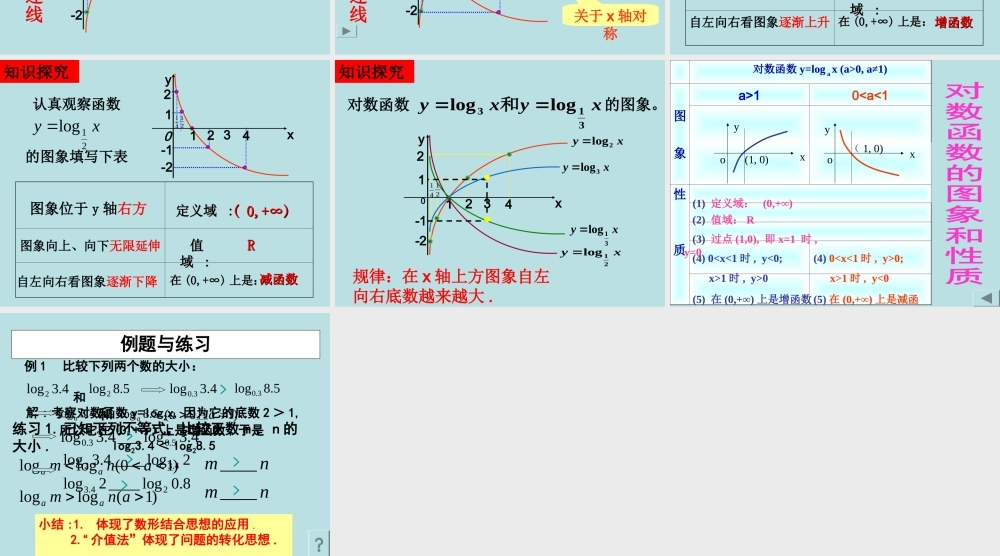
2.2.2 对数函数及其性质（一） zxxk情境引入 用清水漂洗含 1 个单位质量污垢的衣服，若每次能洗去污垢的四分之三，试写出漂洗次数 y 与残留污垢 x 的关系式 . yx)431( y)41(xy41log)0( x 一般地 , 函数 y = loga x(a ＞ 0, 且 a≠ 1) 叫做对数函数 . 其中 x 是自变量 .函数的定义域是（ 0,+∞ ） .1 、对数函数的定义：注意 :对数函数对底数的限制条件：知识探究a ＞ 0, 且 a≠ 1知识探究22 、探究：对数函数、探究：对数函数 ::y = logy = loga a xx （（ aa ＞＞0, 0, 且且 aa≠1)≠1) 的图象与性质的图象与性质在同一坐标系中用描点法画出对数函数 的图象。xyxy212loglog和作图步骤 :: ① 列表 , ② 描点 , ③ 用平滑曲线连接。x1/41/2124…y=log2x-2-1012…列表描点作 y=log2x 的图象连线21-1-21240yx32114知识探究列表描点连线21-1-21240yx32114x1/41/2124xy2log 22 1 1 0 0 -1 -1 -2 -2 -2 -1 0 1 2xy21log这两个函数的图象有什么关系呢？关于 x 轴对称… … … … … … 知识探究定义域 定义域 ::( 0,+∞)( 0,+∞) 值 值 域 域 ::RR增函数增函数在在 (0,+∞)(0,+∞) 上是：上是：认真观察函数y=log2x 的图象填写下表图象位于 y 轴右方图象向上、向下无限延伸自左向右看图象逐渐上升21-1-21240x32114知识探究y认真观察函数的图象填写下表知识探究211421-1-21240yx3xy21log定义域 定义域 ::( 0,+∞)( 0,+∞) 值 值 域 域 ::RR减函数减函数在在 (0,+∞)(0,+∞) 上是：上是：图象位于 y 轴右方图象向上、向下无限延伸自左向右看图象逐渐下降xyxy313loglog和21-1-21240yx32114xy2logxy21logxy3logxy31log知识探究对数函数 的图象。规律：在 x 轴上方图象自左向右底数越来越大 .图象a>100, a≠1)(4) 01 时 , y>0(4) 00; x>1 时 , y<0 (3) 过点 (1,0), 即 x=1 时 , y=0 (1) 定义域： (0,+∞)(2) 值域： Rxyo(1, 0)xyo（ 1, 0)(5) 在 (0,+∞) 上是减函数(5) 在 (0,+∞) 上是增函数例题与练习例 1 比较下列两个数的大小：4.3log25.8log2 和解 : 考察对数函数 y=log2x, 因为它的底数 2 ＞ 1, 所以它在 (0,+∞) 上是增函数 , 于是log23.4 ＜ log28.5 小结 :1. 体现了函数思想的应用 . 2. 体现了分类讨论思想的应用 . 4.3log3.05.8log3.0>4.3loga5.8loga)10(aa且和练习 1. 已知下列不等式，比较正数 m 、 n 的大小 . )10(logloganmaa)1(logloganmaanm____nm____>>4.3log___4.3log5.03.08.0log____2log2log____4.3log24.34.32小结 :1. 体现了数形结合思想的应用 . 2.“ 介值法”体现了问题的转化思想 . >>>