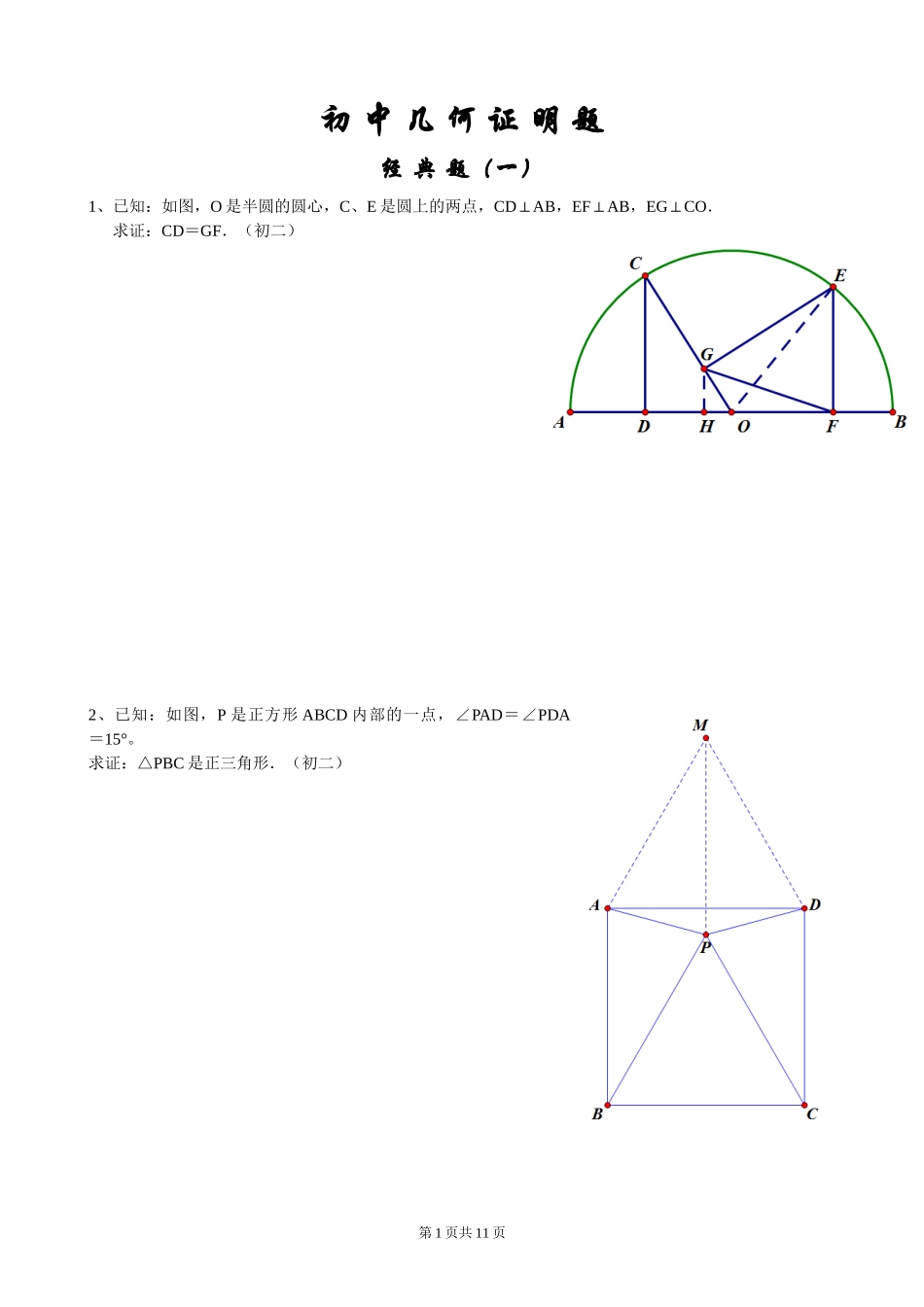
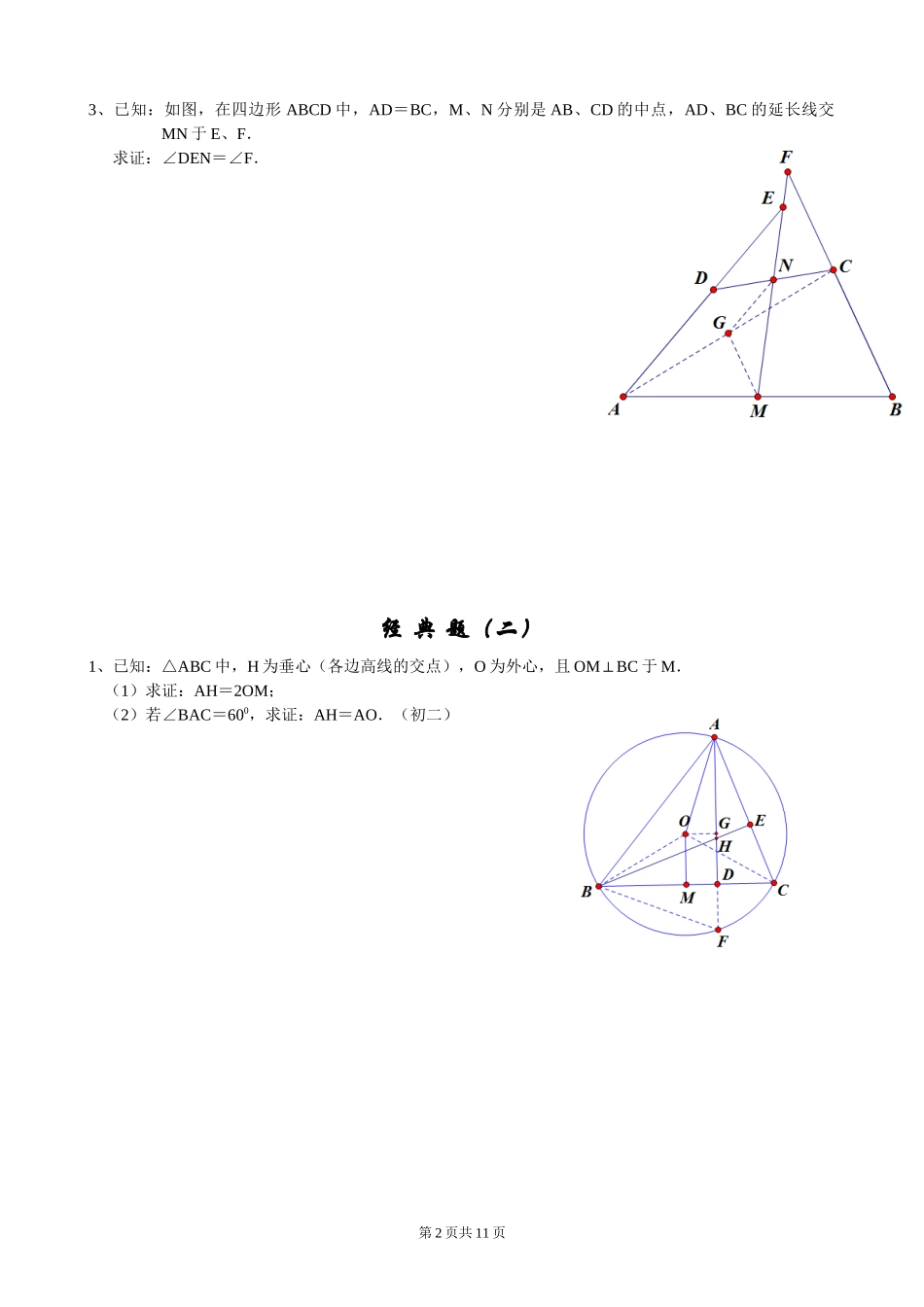
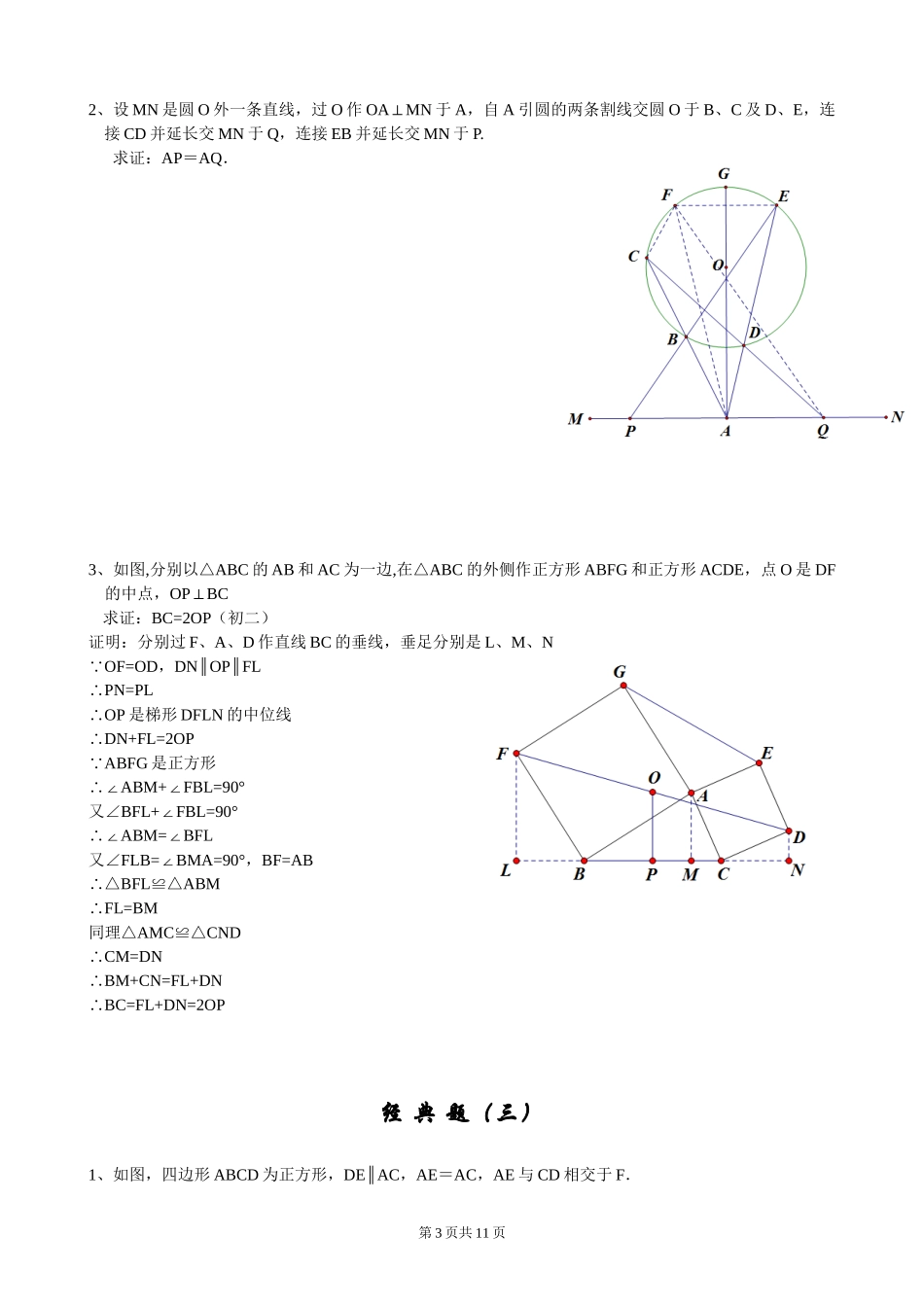
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CDAB⊥,EFAB⊥,EGCO⊥.求证:CD=GF.(初二)2、已知:如图,P是正方形ABCD内部的一点,∠PAD=∠PDA=15°。求证:△PBC是正三角形.(初二)第1页共11页3、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OMBC⊥于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)第2页共11页2、设MN是圆O外一条直线,过O作OAMN⊥于A,自A引圆的两条割线交圆O于B、C及D、E,连接CD并延长交MN于Q,连接EB并延长交MN于P.求证:AP=AQ.3、如图,分别以△ABC的AB和AC为一边,在△ABC的外侧作正方形ABFG和正方形ACDE,点O是DF的中点,OPBC⊥求证:BC=2OP(初二)证明:分别过F、A、D作直线BC的垂线,垂足分别是L、M、NOF=OD ,DNOPFL∥∥PN=PL∴OP∴是梯形DFLN的中位线DN+FL=2OP∴ABFG 是正方形ABM+FBL=90°∴∠∠又∠BFL+FBL=90°∠ABM=BFL∴∠∠又∠FLB=BMA=90°∠,BF=ABBFLABM∴△≌△FL=BM∴同理△AMCCND≌△CM=DN∴BM+CN=FL+DN∴BC=FL+DN=2OP∴经典题(三)1、如图,四边形ABCD为正方形,DEAC∥,AE=AC,AE与CD相交于F.第3页共11页求证:CE=CF.(初二)证明:连接BD交AC于O。过点E作EGAC⊥于GABCD 是正方形BDAC∴⊥又EGAC⊥BDEG∴∥又DEAC∥ODEG∴是平行四边形又∠COD=90°ODEG∴是矩形EG=OD=∴12BD=12AC=12AEEAG=30°∴∠AC=AE ACE=AEC=75°∴∠∠又∠AFD=90°-15°=75°CFE=AFD=75°=AEC∴∠∠∠CE=CF∴2、如图,四边形ABCD为正方形,DEAC∥,且CE=CA,直线EC交DA延长线于F.求证:AE=AF.(初二)证明:连接BD,过点E作EGAC⊥于GABCD 是正方形BDAC∴⊥,又EGAC⊥BDEG∴∥又DEAC∥ODEG∴是平行四边形又∠COD=90°ODEG∴是矩形EG=OD=∴12BD=12AC=12CEGCE=30°∴∠AC=EC 3、设P是正方形ABCD一边BC上的任一点,PFAP⊥,CF平分∠DCE.求证:PA=PF.(初二)证明:过点F作FGCE⊥于G,FHCD⊥于HCDCGHCGF ⊥∴是矩形HCF=GCFFH=FG ∠∠∴HCGF∴是正方形CG=GF∴APFP ⊥APB+FPG=90°∴∠∠APB+BAP=90° ∠∠第4页共11页设AB=x,BP=y,CG=zz:y=(x-y+z):x化简得(x-y)·y=(x-y)·z x-y≠0∴y=z即BP=FGABPPGF∴△≌△CAE=CEA=∴∠∠12∠GCE=15°在△AFC中∠F=180°-FAC-ACF∠∠=180°-FAC-GCE∠∠=180°-135°-30°=15°F=CEA∴∠∠AE=AF∴QCABPEPBACDFPG=BAP∴∠∠又∠FGP=PBA∠FGPPBA∴△∽△FG∴:PB=PG:AB4、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.(初三)证明:过点E作EKBD∥,分别交AC、AF于M、K,取EF的中点H,连接OH、MH、ECEH=FH OHEF∴⊥,∴∠PHO=90°又PCOC⊥,∴∠POC=90°P∴、C、H、O四点共圆HCO=HPO∴∠∠又EKBD∥,∴∠HPO=HEK∠HCM=HEM∴∠∠H∴、C、E、M四点共圆ECM=EHM∴∠∠又∠ECM=EFA∠EHM=EFA∴∠∠HMAC∴∥EH=FH 经典题(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求∠APB的度数.(初二)解:将△ABP绕点B顺时针方向旋转60°得△BCQ,连接PQ则△BPQ是正三角形BQP=60°∴∠,PQ=PB=3在△PQC中,PQ=4,CQ=AP=3,PC=5PQC∴△是直角三角形PQC=90°∴∠BQC=BQP+PQC=60°+90°=150°∴∠∠∠APB=BQC=150°∴∠∠2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)证明:过点P作AD的平行线,过点A作PD的平行线,两平行线相交于点E,连接BEPEAD ∥,AEPD∥ADPE∴是平行四边形PE=AD∴,又ABCD是平行四边形AD=BC∴PE=BC∴又PEAD∥,ADBC∥PEBC∴∥BCPE∴是平行四边形第5页共11页EM=KM∴EKBD ∥∴OBEM=AOAM=ODKMOB=OD∴又AO=CO∴四边形ABCD的对角线互相平分ABCD∴是平行四边形AB=DC∴,BC=AD又∠ADP=ABP∠AEP=ABP∴∠∠∴A、E、B、P四点共圆BEP=PAB∴∠∠PAB=PCB∴∠∠ECBADGDEABCPHGFDACBEPBEP=PCB∴∠∠ADPE 是平行四边形ADP=AEP∴∠∠3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·B...