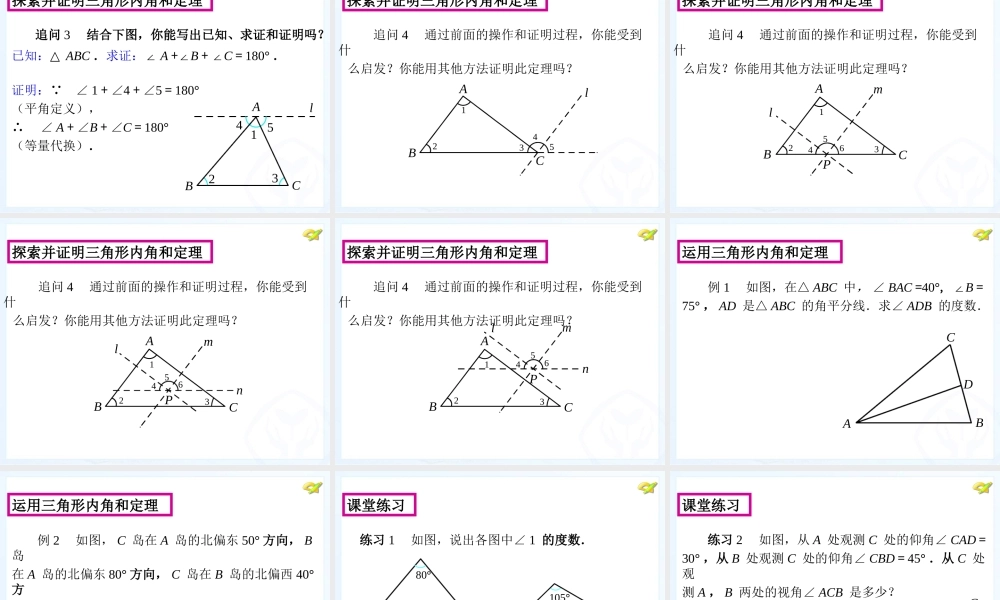
八年级 上册11.2 与三角形有关的角 (第 1 课时)课件说明• 三角形内角和定理是本章的重要内容,也是“图形 与几何”必备的知识基础.它从“角”的角度刻画 了三角形的特征.三角形内角和定理的探究体现了 由实验几何到论证几何的研究过程,同时也说明了 证明的必要性.课件说明• 三角形内角和定理的证明以平行线的相关知识为基 础.定理的验证方法——剪图、拼图,不仅可以说 明证明的必要性,而且也可以从中获得添加辅助线 的思路和方法.定理的证明思路是得出三角形的三 个内角与组成平角的三个角分别相等. • 学习目标: 1 .探索并证明三角形内角和定理. 2 .能运用三角形内角和定理解决简单问题.• 学习重点: 探索并证明三角形内角和定理,体会证明的必要性. 课件说明方法:度量、剪拼图、折叠 探索并证明三角形内角和定理BBCCAAABBC 问题 1 在小学我们已经知道任意一个三角形三个内角的和等于 180° ,你还记得是怎么发现这个结论的吗?请大家利用手中的三角形纸片进行探究. 问题 1 在小学我们已经知道任意一个三角形三个内角的和等于 180° ,你还记得是怎么发现这个结论的吗?请大家利用手中的三角形纸片进行探究. 探索并证明三角形内角和定理AABBCABBCC方法:度量、剪拼图、折叠 问题 1 在小学我们已经知道任意一个三角形三个内角的和等于 180° ,你还记得是怎么发现这个结论的吗?请大家利用手中的三角形纸片进行探究. 探索并证明三角形内角和定理ABC方法:度量、剪拼图、折叠 探索并证明三角形内角和定理 追问 1 运用度量的方法,得出的三个内角的和都是 180° 吗?为什么?测量可能会有误差. 探索并证明三角形内角和定理 追问 2 通过度量、剪拼图或折叠的方法验证了手中的三角形纸片的三个内角和等于 180° ,但我们手中的三角形只是所有三角形中有限的几个,而形状不同的 三角形有无数多个,我们如何能得出“所有的三角形的三个内角的和都等于 180°” 这个结论呢?需要通过推理的方法去证明. 探索并证明三角形内角和定理 问题 2 你能从以上的操作过程中受到启发,想出 证明“三角形内角和等于 180°” 的方法吗?探索并证明三角形内角和定理 追问 1 在下图中,∠ B 和∠ C 分别拼在∠ A 的左右,三个角合起来形成一个平角,出现了一条过点 A 的直线 l ,直线 l 与边 BC 有什么位置关系?直线 l 与边 BC 平行. BBCCAl探索并证...