解一元一次方程一移项VIP免费

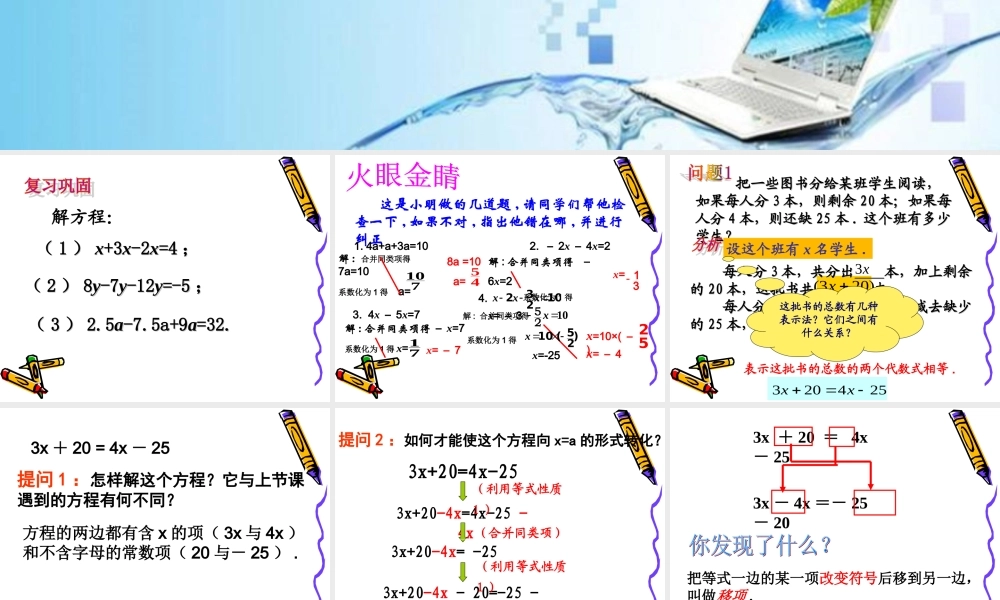
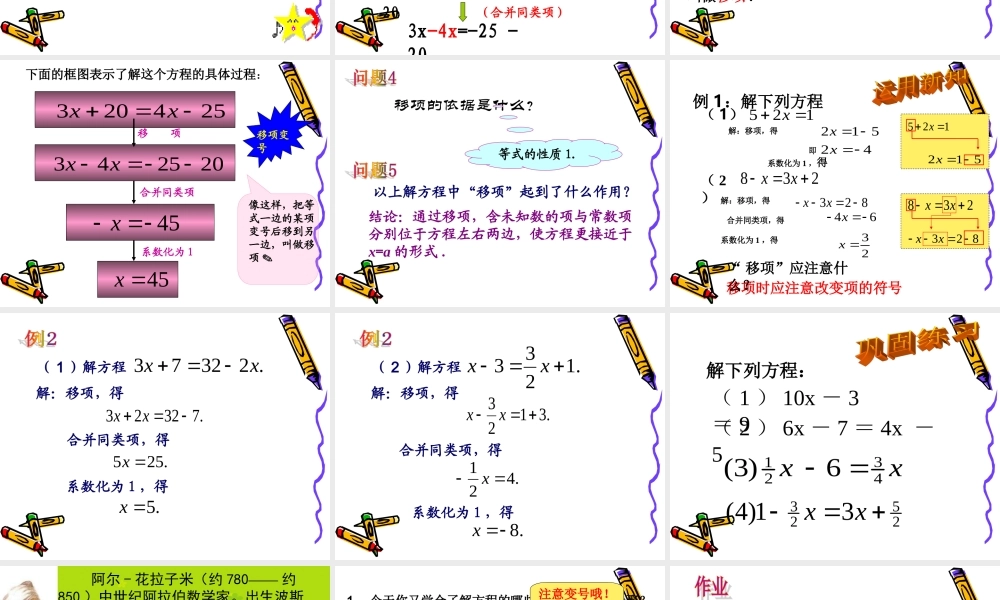
第三章 一元一次方程3.2 3.2 解一元一次方程解一元一次方程（一）（一）—— 合并同类项与移项解方程：（（ 11 ）） xx+3+3xx-2-2xx=4=4 ；；（（ 22 ）） 88yy-7-7yy-12-12yy=-5=-5 ；；（（ 33 ）） 2.52.5aa-7.5a+9-7.5a+9aa=32.=32. 这是小明做的几道题 , 请同学们帮他检查一下 , 如果不对 , 指出他错在哪 , 并进行纠正1. 4a+a+3a=102. － 2x － 4x=23. 4x － 5x=74. x=-25解 : 合并同类项得 －6x=2 系数化为 1 得 x= － 3107解 : 合并同类项得 7a=10系数化为 1 得 a= x=3117解 : 合并同类项得 － x=7系数化为 1 得 x=x= － 78a =10 a= 54x=10×( － )52x= － 410x25解 : 合并同类项得 10232xxx系数化为 1 得)25(10 x 把一些图书分给某班学生阅读，把一些图书分给某班学生阅读，如果每人分如果每人分 33 本，则剩余本，则剩余 2020 本；如果每本；如果每人分人分 44 本，则还缺本，则还缺 2525 本本 .. 这个班有多少这个班有多少学生？学生？ 每人分每人分 33 本，共分出本，共分出 本，加上剩余本，加上剩余的的 2020 本，这批书共本，这批书共 本本 .. 每人分每人分 44 本，需要本，需要 本，减去缺少本，减去缺少的的 2525 本，这批书共本，这批书共 本本 ..)203(xx4x3)254(x设这个班有 x 名学生 .这批书的总数有几种表示法？它们之间有什么关系？表示这批书的总数的两个代数式相等 .254203xx提问 1 ：怎样解这个方程？它与上节课遇到的方程有何不同？ 3x ＋ 20 = 4x － 25方程的两边都有含 x 的项（ 3x 与 4x ）和不含字母的常数项（ 20 与－ 25 ） .3x+20=4x-253x+20-4x=4x-25 －4x3x+20-4x= -253x+20-4x － 20=-25 －203x-4x=-25 －20（合并同类项）（利用等式性质1 ） （利用等式性质1 ） （合并同类项）提问 2 ：如何才能使这个方程向 x=a 的形式转化？3x ＋ 20 ＝ 4x － 253x － 4x ＝－ 25 － 20把等式一边的某一项改变符号后移到另一边，叫做移项 . 254203xx202543xx45 x45x移 项合并同类项系数化为 1像这样，把等式一边的某项变号后移到另一边，叫做移项 .移项变号下面的框图表示了解这个方程的具体过程：以上解方程中“移项”起到了什么作用？结论：通过移项，含未知数的项与常数项分别位于方程左右两边，使方...