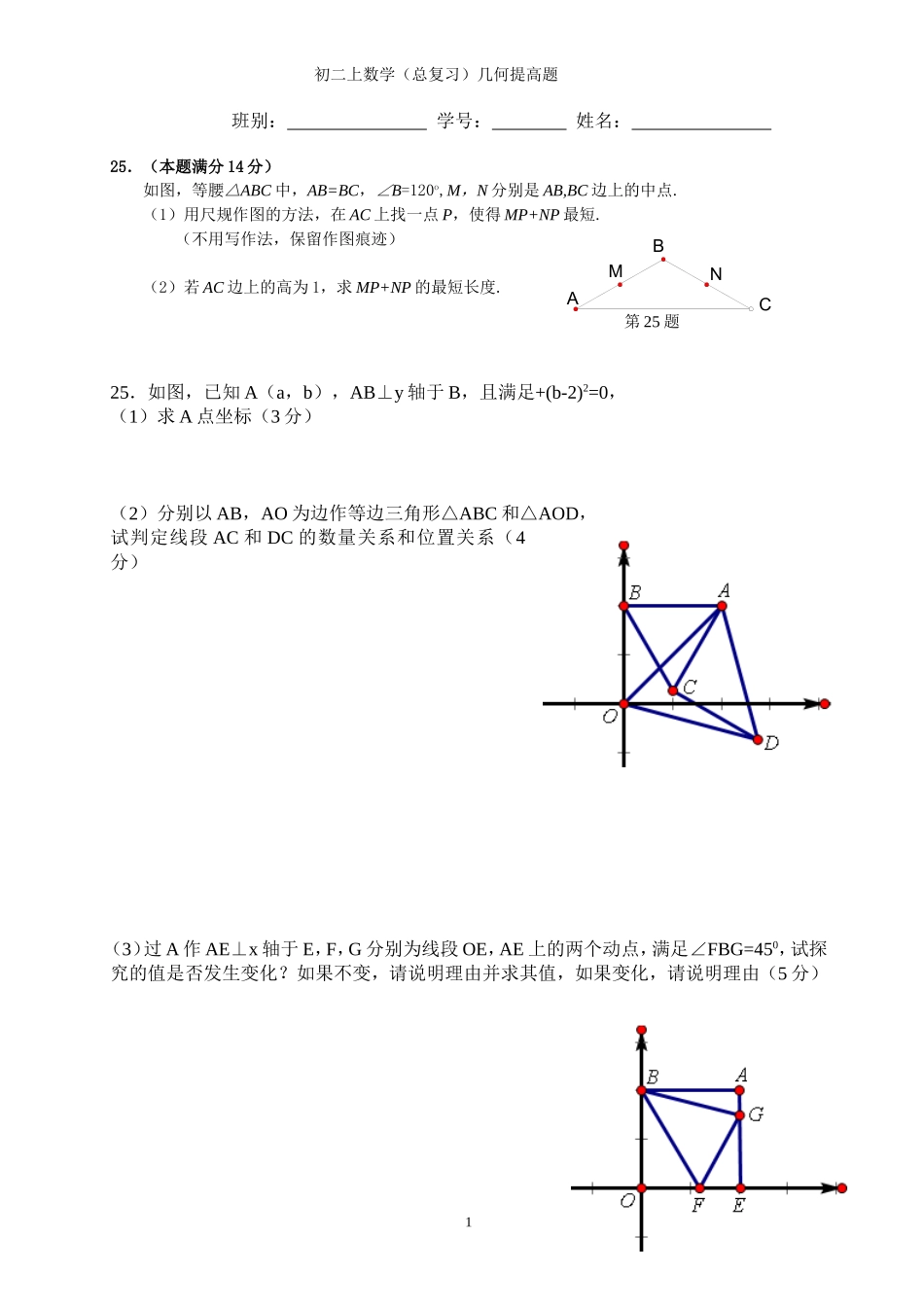
初二上数学(总复习)几何提高题班别: 学号: 姓名: 25.(本题满分 14 分)如图,等腰△ABC 中,AB=BC,∠B=120o,M,N 分别是 AB,BC 边上的中点.(1)用尺规作图的方法,在 AC 上找一点 P,使得 MP+NP 最短.(不用写作法,保留作图痕迹)(2)若 AC 边上的高为 1,求 MP+NP 的最短长度.25.如图,已知 A(a,b),AB⊥y 轴于 B,且满足+(b-2)2=0,(1)求 A 点坐标(3 分)(2)分别以 AB,AO 为边作等边三角形△ABC 和△AOD,试判定线段 AC 和 DC 的数量关系和位置关系(4分)(3)过 A 作 AE⊥x 轴于 E,F,G 分别为线段 OE,AE 上的两个动点,满足∠FBG=450,试探究的值是否发生变化?如果不变,请说明理由并求其值,如果变化,请说明理由(5 分)1NMCAB第 25 题初二上数学(总复习)几何提高题26、(12 分),如图,在平面直角坐标系中,△AOB 为等腰直角三角形,A(4,4)(1)求 B 点坐标;AOyxB(2)若 C 为 x 轴正半轴上一动点,以 AC 为直角边作等腰直角△ACD,∠ACD=90°连 OD,求∠AOD 的度数;AODyxBC(3)过点 A 作 y 轴的垂线交 y 轴于 E,F 为 x 轴负半轴上一点,G 在 EF 的延长线上,以 EG 为直角边作等腰 Rt△EGH,过 A 作 x 轴垂线交 EH 于点 M,连 FM,等式=1 是否成立?若成立,请证明:若不成立,说明理由.AOGyxFMHE2初二上数学(总复习)几何提高题26、(1)作 AE⊥OB 于 E, A(4,4),∴OE=4………………(1 分), △AOB 为等腰直角三角形,且 AE⊥OB,∴OE=EB=4…………(2 分),∴OB=8,∴B(8,0)………………(3 分)(2)作 AE⊥OB 于 E,DF⊥OB 于 F, △ACD 为等腰直角三角形,∴AC=DC,∠ACD=90°即∠ACF+∠DCF=90°, ∠FDC+∠DCF=90°,∴∠ACF=∠FDC,又 ∠DFC=∠AEC=90°,∴△DFC≌△CEA(5 分),∴EC=DF,FC=AE, A(4,4),∴AE=OE=4,∴FC=OE,即OF+EF=CE+EF,∴OF=CE,∴OF=DF,∴∠DOF=45°……………………(6 分) △AOB 为等腰直角三角形,∴∠AOB=45°,∴∠AOD=∠AOB+∠DOF=90°…………(7 分)方 法 二 : 过 C 作 CK⊥x 轴 交 OA 的 延 长 线 于 K , 则 △ OCK 为 等 腰 直 角 三 角 形 ,OC=CK , ∠ K=45° , 又 △ ACD为 等 腰Rt△ , ∴ ∠ ACK=90° -∠OCA=∠DCO,AC=DC,∴△ACK≌△DCO(SAS),∴∠DOC=∠K=45°...