圆柱坐标系和球坐标系VIP免费

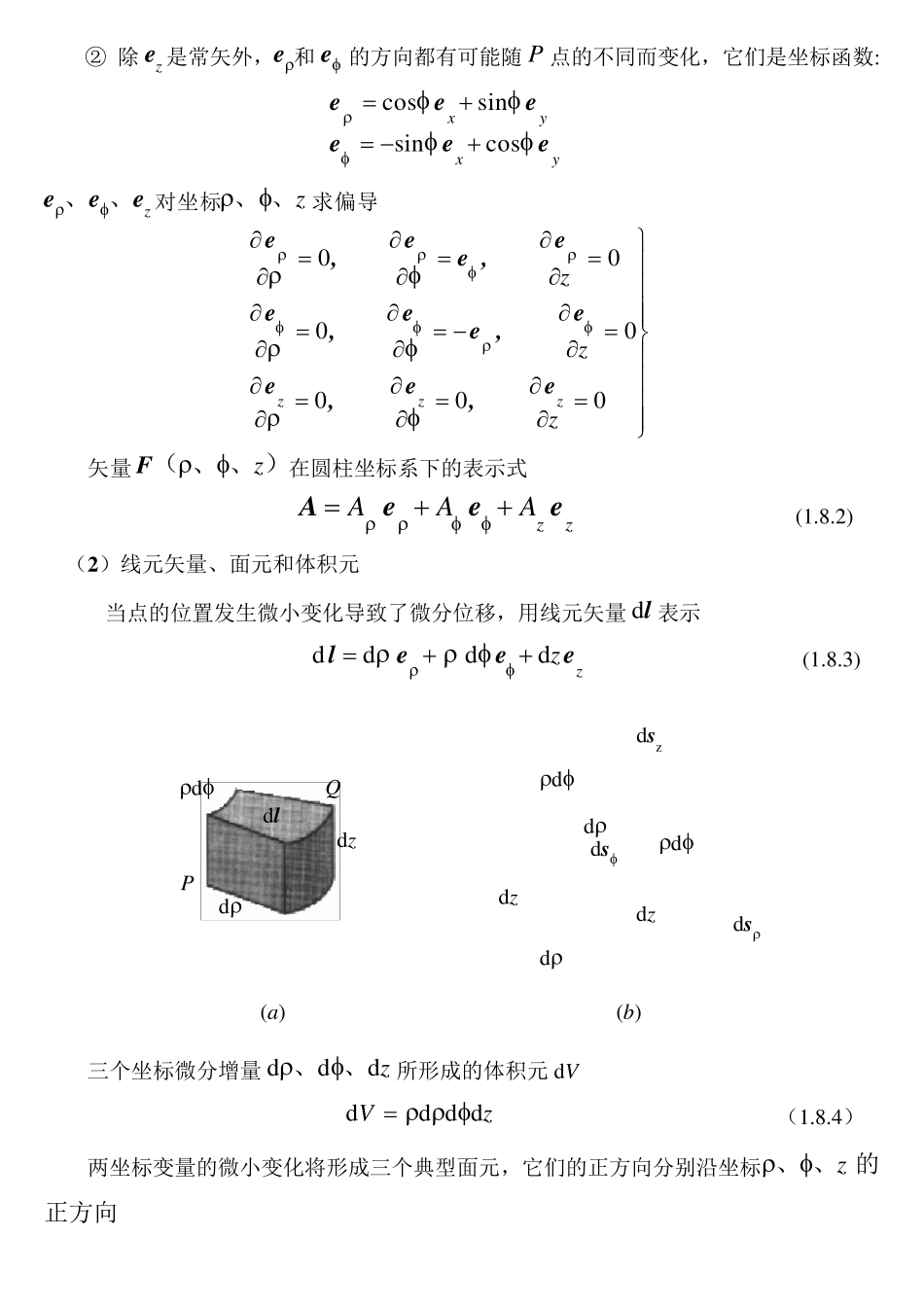
1 .8 圆柱坐标系与球坐标系 1 .8 .1 圆柱坐标系 （1 ）建立圆柱坐标系 空间任一点P 的位置由坐标（，，z）确定，如图（a）所示。其中： ①  是P 点到z 轴的距离，即位置矢量r 在xoy 平面上的投影； ②  是正x 轴转到半平面oABC 的方位角(0≤ ≤2)； ③ z 是位置矢量r 在z 轴上的投影，即P 点到xoy 平面的距离。 这三个坐标确定之后，就确定了三个坐标面： ① 以 z 为轴、为半径的圆柱面； ② 正xoz 半平面绕 z 轴逆时钟旋转角度所得半平面； ③ 距xoy 平面为 z 的平行平面。 这三个坐标面交汇于 P 点，且在P 点处相互正交。为反映这一特征，在P 点处分别沿三个坐标增加的方向各取一个单位矢量e、e和 ez，三单位矢量有以下特点： ① 三个单位矢量相互正交，且满足右手关系 e  e  ez e  ez  e （1.8.1） ez  e  e (a) (b)  y    o x cos ex cos ey sin ex sin ey e e P′ z = 常数(平面)  =常数(平面)  =常数 (圆柱面)  z y x P(,,z) e ez e r o A B C ② 除 ez是常矢外，e和 e 的方向都有可能随 P 点的不同而变化，它们是坐标函数: yxyxeeeeeecossinsincos e、e、ez对坐标、、z 求偏导 0000000zzzzzze,e,ee,ee,ee,ee,e 矢量 F（、、z）在圆柱坐标系下的表示式 zzAAAeeeA (1.8.2) （2 ）线元矢量、面元和体积元 当点的位置发生微小变化导致了微分位移，用线元矢量 dl 表示 zzeeeldddd (1.8.3) 三个坐标微分增量 d、d、dz 所形成的体积元 dV zVdddd （1.8.4） 两坐标变量的微小变化将形成三个典型面元，它们的正方向分别沿坐标、、z 的正方向 (a) (b) dz d d P Q dl dz d d dz d d ds z ds  ds  dddddddddzSzSzS (1.8.5) （3 ）圆柱坐标系中的三度表达式 对于连续、可微的标量场 f (、、z)，按多元函数的全微分链式法则表示微增量 zzffffdddd 作改写 zzzzfffzzffffeeeeeeddd1dddd...