圆锥曲线——仿射变换VIP免费

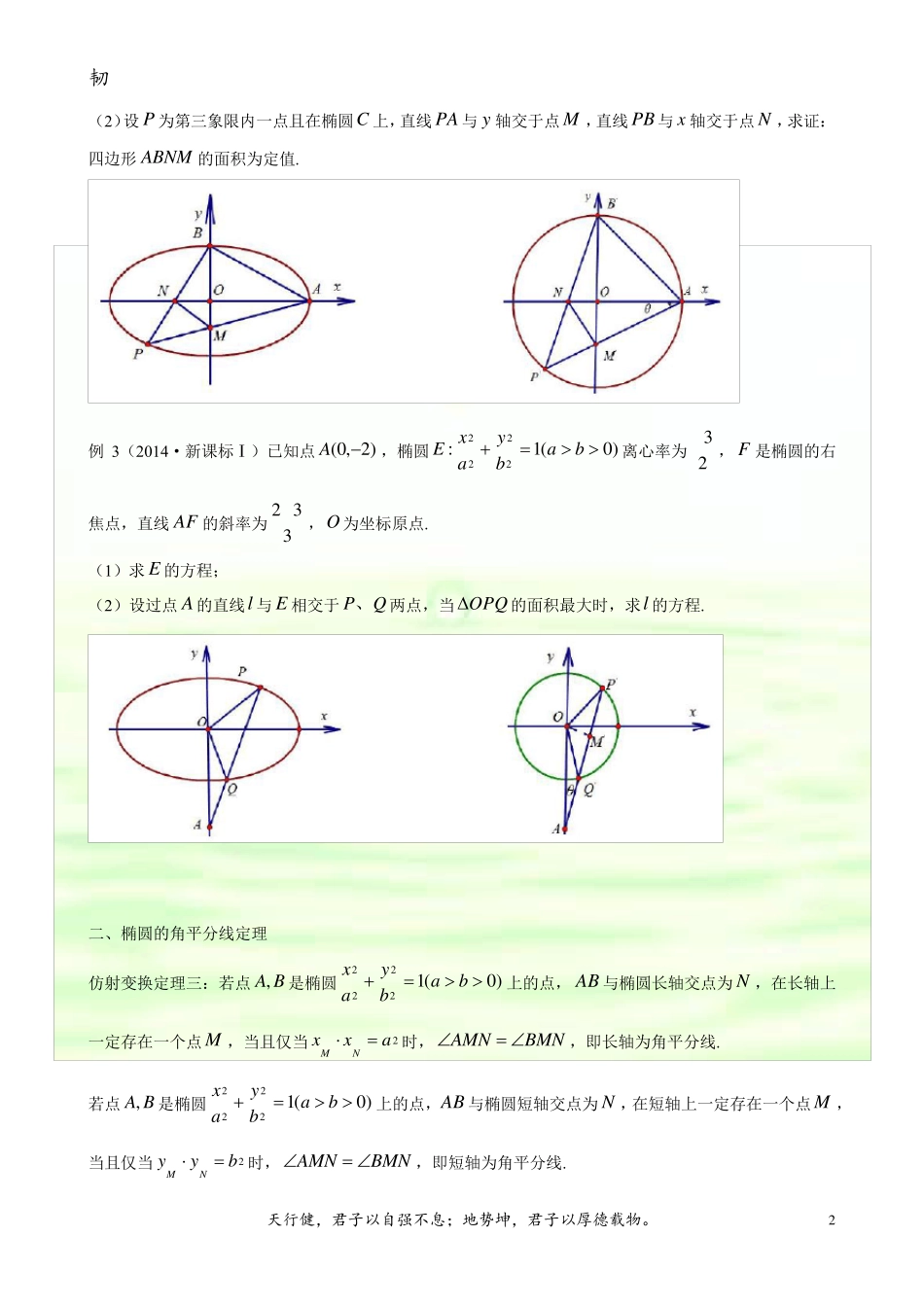
韧 天行健，君子以自强不息；地势坤，君子以厚德载物。 1 仿射变换 一、将坐标进行伸缩变换，实现化椭为圆 仿射变换定理一：若经过椭圆的对称中心的直线构成的直径三角形，则两条弦的斜率乘积22abkkBCAC. 仿射变换定理二：baSS '（拉伸短轴）；abSS ''（压缩长轴）. 拉伸短轴后点的坐标变化：),(),(00'00ybaxAyxA，横坐标不变，纵坐标拉伸ba倍. 斜率的变化：如图纵坐标拉伸了ba倍，故 kbak '，由于1''''CBCAkk. 22''''abkabkabkkCBCABCAC，'''CBAABCSabS（水平宽不变，铅垂高缩小）. 压缩长轴后点的坐标变化：),(),(00'00yxabAyxA，纵坐标不变，横坐标缩小ab倍. 斜率的变化：如图横坐标缩小了ab倍，故 kbak '，由于1''''CBCAkk. 22''''abkabkabkkCBCABCAC，'''CBAABCSbaS（水平宽扩大，铅垂高不变）. 例1（2013·新课标）椭圆134:22 yxC的左、右顶点分别为21AA、，点P 在C 上且直线2PA 斜率的取值范围是1,2 ，那么直线1PA 斜率的取值范围是（ ） A . 43,21； B. 43,83； C. 1,21； D. 1,43. 例2（2016·北京）已知椭圆1:2222 byaxC过点)1,0(),0,2(BA两点. （1）求椭圆C 的方程及离心率； 韧 天行健，君子以自强不息；地势坤，君子以厚德载物。 2 （2）设P 为第三象限内一点且在椭圆C 上，直线PA 与y 轴交于点M ，直线PB 与x 轴交于点N ，求证：四边形ABNM 的面积为定值. 例3（2014·新课标Ⅰ）已知点 )2,0( A，椭圆)0(1:2222babyaxE离心率为23，F 是椭圆的右焦点，直线AF 的斜率为332，O 为坐标原点. （1）求E 的方程； （2）设过点A 的直线l 与E 相交于QP、两点，当 OPQ的面积最大时，求l 的方程. 二、椭圆的角平分线定理 仿射变换定理三：若点BA,是椭圆)0(12222babyax上的点，AB 与椭圆长轴交点为N ，在长轴上一定存在一个点M ，当且仅当2axxNM时，BMNAMN，即长轴为角平分线. 若点BA,是椭圆)0(12222babyax上的点，AB 与椭圆短轴交点为N ，在短轴上一定存在一个点M ，当且仅当2byyNM时，BMNAMN，即短轴为角平分线. 韧 天行健，君子以自强不息；地势坤，君子以厚德载物。 3 例4（2018·全国卷Ⅰ）设椭圆12:22 yxC的右焦点为 F ，过 F 的直线l 与C 交于BA,两点，点M...