Polya定理VIP免费

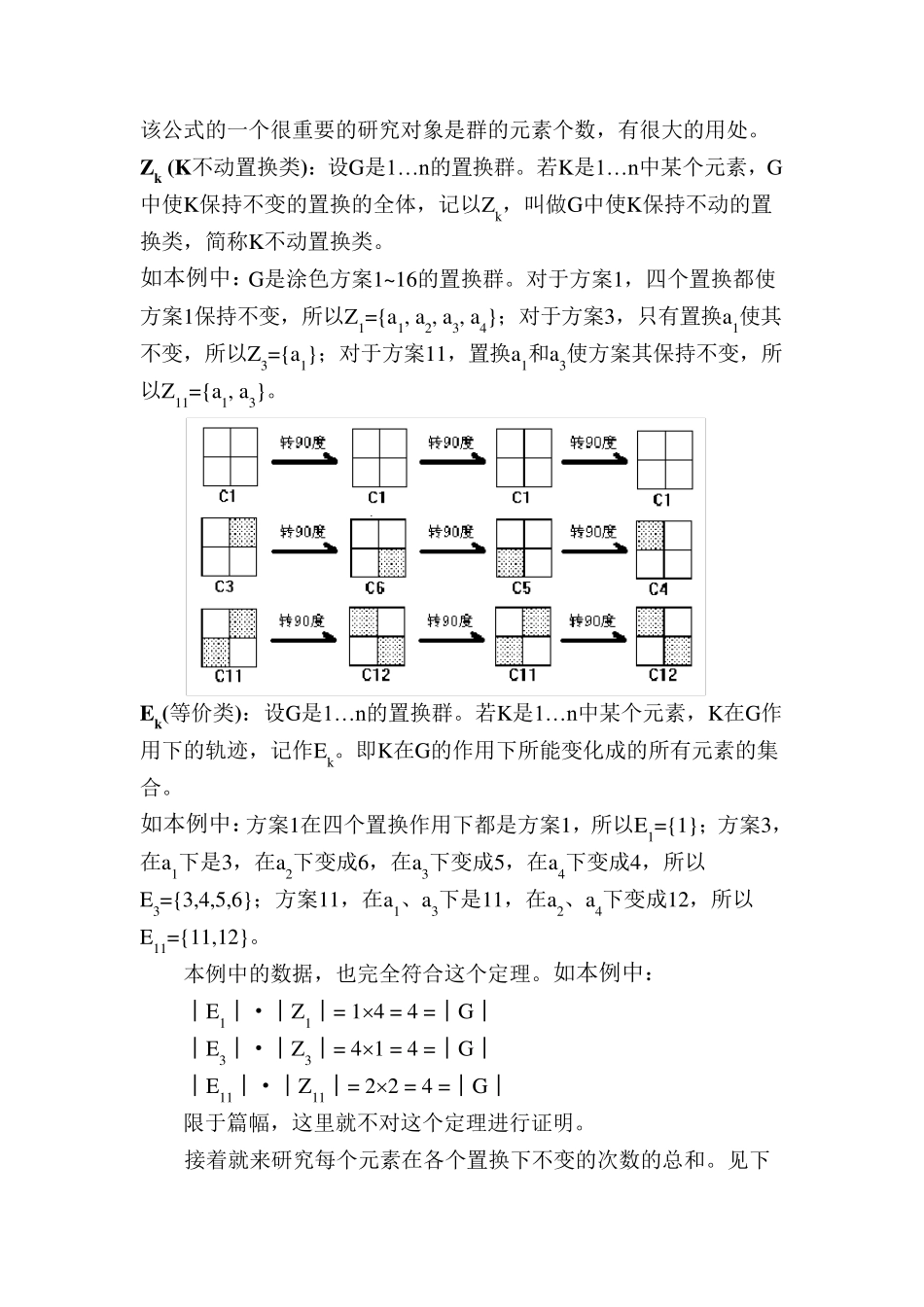
Póly a原理及其应用 华东师大二附中 符文杰 Pólya原理是组合数学中，用来计算全部互异的组合状态的个数的一个十分高效、简便的工具。下面，我就向大家介绍一下什么是Pólya原理以及它的应用。请先看下面这道例题： 【例题1】 对2*2的方阵用黑白两种颜色涂色，问能得到多少种不同的图像？经过旋转使之吻合的两种方案，算是同一种方案。 【问题分析】 由于该问题规模很小，我们可以先把所有的涂色方案列举出来。 一个2*2的方阵的旋转方法一共有4种：旋转0度、旋转90度、旋转180度和旋转270度。(注：本文中默认旋转即为顺时针旋转) 我们经过尝试，发现其中互异的一共只有6种：C3、C4、C5、C6是可以通过旋转相互变化而得，算作同一种；C7、C8、C9、C10是同一种；C11、C12是同一种；C13、C14、C15、C16也是同一种； C1和C2是各自独立的两种。于是，我们得到了下列6种不同的方案。 但是，一旦这个问题由2*2的方阵变成20*20甚至200*200的方阵，我们就不能再一一枚举了，利用Pólya原理成了一个很好的解题方法。在接触Pólya原理之前，首先简单介绍Pólya原理中要用到的一些概念。 群：给定一个集合G={a,b,c,… }和集合G上 的二 元 运 算，并 满 足 : (a) 封闭性：a,bG, cG, a＊b=c。 (b) 结合律：a,b,cG, (a＊b)＊c=a＊(b＊c)。 (c) 单位元：eG, aG, a＊e=e＊a=a。 (d) 逆元：aG, bG, a＊b=b＊a=e，记b=a-1。 则称集合G在运算＊之下是一个群，简称G是群。一般a＊b简写为ab。 置换：n个元素1,2,… ,n之间的一个置换naaan2121表示1被1到n中的某个数a1取代，2被1到n中的某个数a2取代，直到n被1到n中的某个数an取代，且a1,a2,… ,an互不相同。本例中有4个置换： 转0 a1=1615141312111098765432116151413121110987654321 转90 a2=1514131611129871054362116151413121110987654321 转180 a3=1413161512118710943652116151413121110987654321 转270 a4=1316151411127109836542116151413121110987654321 置换群：置换群的元素是置换，运算是置换的连接。例如： 1342432113424213421343211234432142134321 可以验证置换群满足群的四个条件。 本题中置换群G={转0、转90、转180、转27...