成考数学必背的公式VIP免费

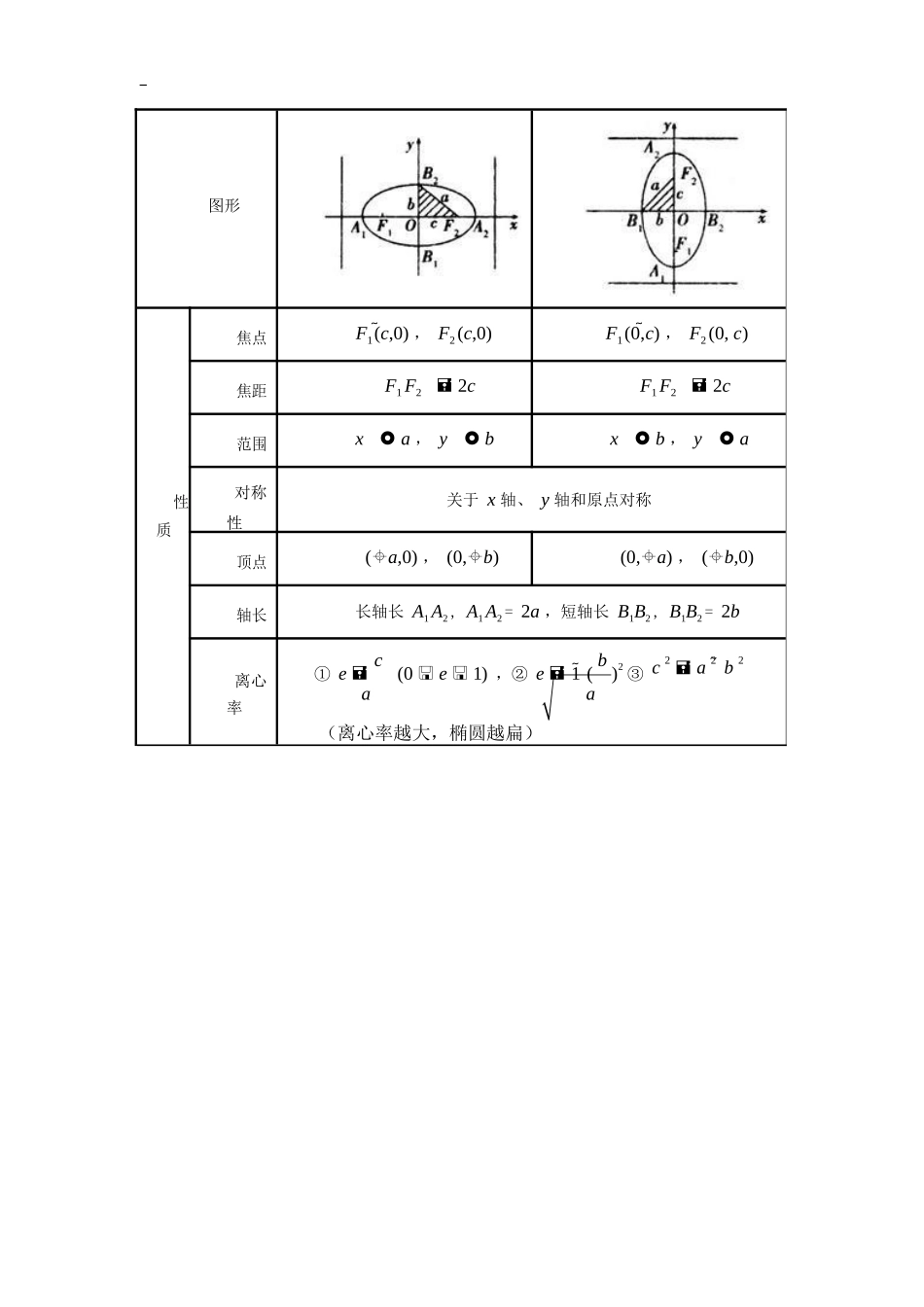
斜率公式k  y2  y1 （ P (x , y ) 、 P (x , y ) ）.x  x11122221等差数列和公式Sn=n(a1+an)/2=na1+n(n-1)/2 d 等比数列求和公式q≠1 时 Sn=a1(1-q^n)/(1-q)=(a1-anq)/(1-q) q=1 时 Sn=na1(a1 为首项,an 为第 n 项,d 为公差,q 为等比)余弦定理对于任意三角形，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的两倍积，若三边为 a，b，c 三角为 A，B，C ，正弦定理asin A bsin B csin C 2R （ R 为ABC 外接圆半径）倍角公式 正弦二倍角公式：0.sin2α=2cosαsinα1.Cos2a=Cosa^2-Sina^2=[1-tana^2]/[1+tana^2]2.Cos2a=1-2Sina^23.Cos2a=2Cosa^2-1标准方程x 2a 2y 2b 21 (a b 0)y 2a 2x 2b 21(a b 0)sin( )  sin cos  cos sin  sin( )  sin cos  cos sin  cos( )  cos cos  sin sin  cos( )  cos cos  sin sin tan( ) tan( ) tan tan  1  tan tan tan tan  1  tan tan tan 22 tan 1  tan 2点到线的距离公式：P(x0,y0)到直线 Ax+By+C=0求根公式平面向量的运算法则。1）设 a ＝ (x1 , y1 ) ， b ＝ (x2 , y2 ) ，则 a + b ＝ (x1  x2 , y1  y2 ) 。2）设 a ＝ (x1 , y1 ) ， b ＝ (x2 , y2 ) ，则 a - b ＝ (x1  x2 , y1  y2 ) 。3）设点 A (x1 , y1 ) ，B (x2 , y2 ) ，则 AB  OB  OA  (x2  x1 , y2  y1 ) 。4）设 a ＝ (x, y), R ，则a ＝ (x,y) 。5）设 a ＝ (x1 , y1 ) ， b ＝ (x2 , y2 ) ，则 a  b ＝ (x1 x2  y1 y2 ) 。图形性质焦点F1 (c,0) ， F2 (c,0)F1 (0,c) ， F2 (0, c)焦距F1 F2  2cF1 F2  2c范围x a ， y bx b ， y a对称性关于 x 轴、 y 轴和原点对称顶点(a,0) ， (0,b)(0,a) ， (b,0)轴长长轴长 A1 A2 , A1 A2 = 2a ，短轴长 B1B2 , B1B2 = 2b离心率① e  c (0  e  1) ，② e  1 ( b )2 ③ c 2  a 2  b 2aa（离心率越大，椭圆越扁）1.双曲线的方程及几何性质标准方程x2  y2 a2b2 1(a  0, b  0)y2  x2 1(a0,b0)a2b2图形焦点F1（-c，0），F2（c，0）F1（0，-c），F2（0，c）顶点A1（a，0），A2（-a，0）A1（0，a），A2（0，-a）对称轴实轴 2a，虚轴 2b，实轴在 x 轴上，c2=a2+b2实轴 2a，虚轴 2b，实轴在 y 轴上，c2=a2+b2离心率e  c  | MF2 |a| MD |e  c  | MF2 |a| MD |准线方程a2a2l1 : x  c , l2 : x   c准线间距离为 2a2ca2a22a2l1 : y  c , l2 : y   c 准线间距离为 c渐近线方程x  y  0, x  y  0ababx  y  0, x  y  0baba方程设抛物线 y 2  2 px p  0性质焦点范围对称性顶点离心率准线通径F  p ,0 2 x  0关于 x轴对称原点e  1x   p22 p