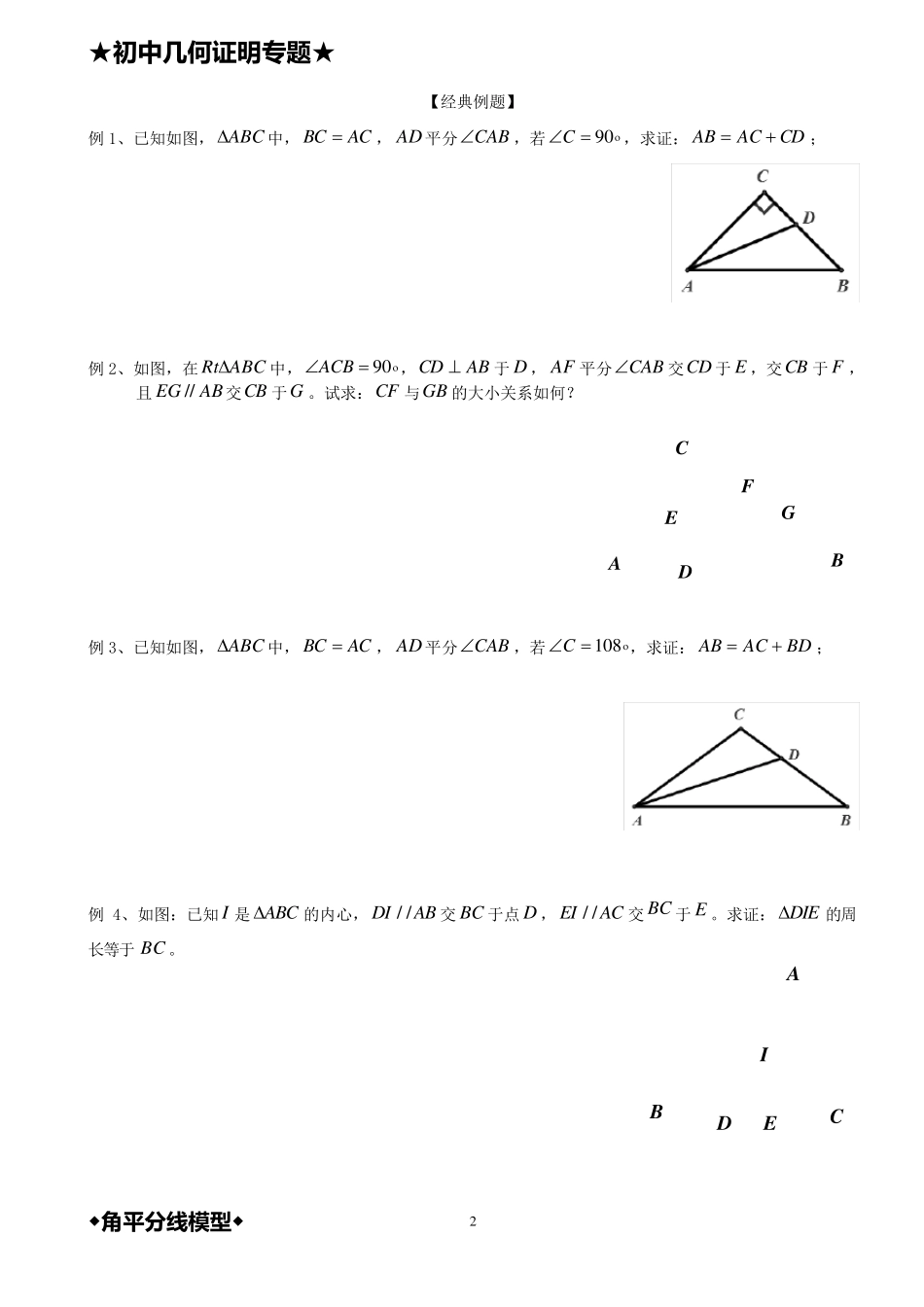
★初 中 几 何 证 明 专题 ★ ◆角 平 分 线 模 型 ◆ 1 BPCABPCABPCAFENBMPCADABC几 何 证 明 ——角 平 分 线 模 型 (中 级) 【知识要点】 1、角平分线: (1)角平分线性质定理:角平分线上的点到这个角的两边的距离相等(作用:证明两条线段相等); (2)逆定理:在角的内部,到角的两边距离相等的点在这个角的角平分线上。(作用:证明两角相等或一条射线是一个角的角平分线)。 2、角平分线常见用法(或辅助线作法): ①垂两边:如图1,已知BP 平分ABC,过点P作PAAB,PCBC,则PAPC。 ②截两边:如图2,已知BP 平分MBN,点A BM 上,在BN 上截取BCBA,则ABP≌CBP。 ③角平分线+平行线→等腰三角形: 如图3,已知BP 平分ABC,/ /PAAC ,则ABAP; 如图4,已知BP 平分ABC,/ /EFPB ,则BEBF。 (1) (2) (3) (4) ④三线合一(利用角平分线+垂线→等腰三角形): 如图5,已知AD 平分BAC,且 ADBC,则ABAC,BDCD。 (5) 3、角平分线比例定理 如图6,AD 为 ABC的角平分线,则ABBDACCD或ABACBDCD。 (6 ) CDAB★初 中 几 何 证 明 专题 ★ ◆角 平 分 线 模 型 ◆ 2 【经典例题】 例 1、已知如图, ABC中, BCAC, AD平分CAB,若9 0C,求证:CDACAB; 例 2、如图,在ABCRt中,9 0ACB,ABCD 于 D , AF 平分CAB交CD 于 E ,交CB 于 F ,且ABEG //交CB 于G 。试求:CF 与GB 的大小关系如何? ECABDFG 例 3、已知如图, ABC中, BCAC, AD 平分CAB,若1 0 8C,求证:BDACAB; 例 4、如图:已知 I 是 ABC的内心,/ /DIAB 交 BC 于点 D ,/ /EIAC 交 BC 于 E 。求证: DIE的周长等于 BC 。 ABCIDE ★初 中 几 何 证 明 专题 ★ ◆角 平 分 线 模 型 ◆ 3 例5、如图:已知在ABC中,ABC的平分线与ACB的外角平分线交于点D ,DE∥ BC ,交AB 于点E,交AC 于点F ,求证:FCBEEF。 FEDABCM 例6、如图,已知ABC中CDACABBAC,,9 0垂直于ABC的平分线BD于D ,BD交AC 于E,求证: CDBE2。 EDABC ★初 中 几 何 证 明 专 题 ★ ◆角 平 分 线 模 型 ◆ 4 【提升训练】 1、如图,已知ABC的周长是 OCOB,,21分别平分ABC和ACB, BCOD 于D ,且...