极坐标和直角坐标的互化VIP免费

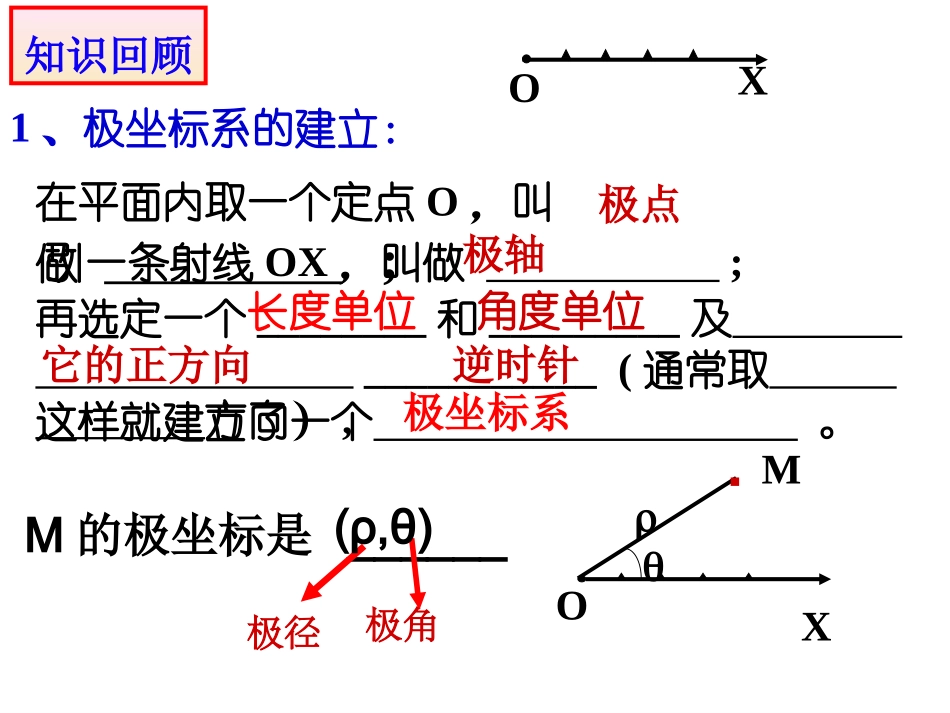
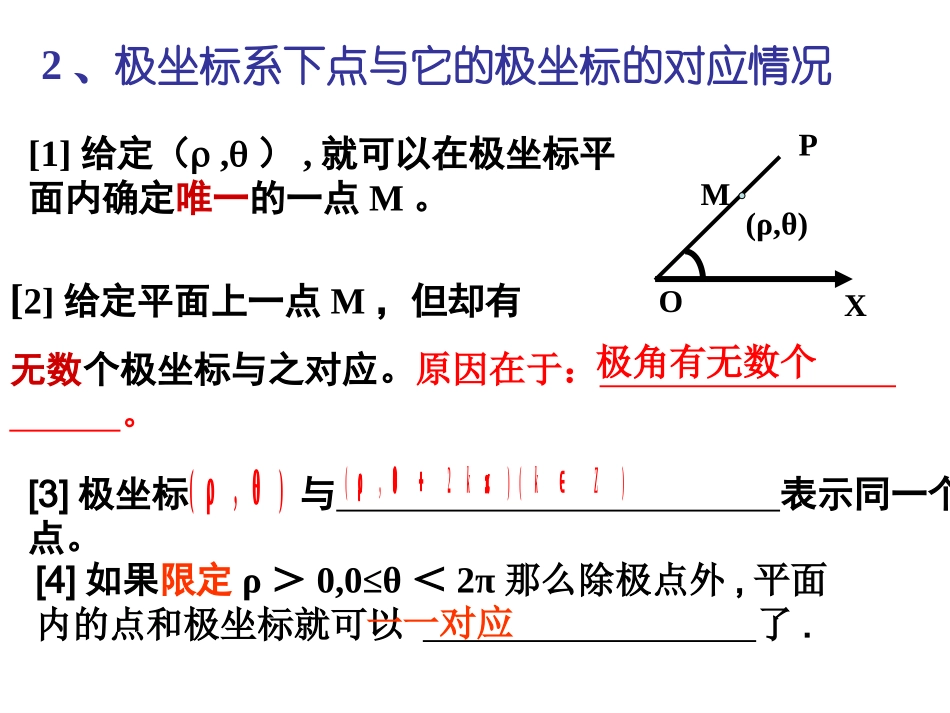
极坐标与直角坐标极坐标与直角坐标的互化的互化1、极坐标系的建立：在平面内取一个定点O，叫做;引一条射线OX，叫做;再选定一个________和_________及___________(通常取方向）,这样就建立了一个。XO知识回顾极点极轴它的正方向逆时针极坐标系M的极坐标是______极径极角(ρ,θ)XOM·角度单位长度单位2、极坐标系下点与它的极坐标的对应情况[1]给定（,）,就可以在极坐标平面内确定唯一的一点M。[2]给定平面上一点M，但却有无数个极坐标与之对应。原因在于：。OXPM(ρ,θ)[4]如果限定ρ＞0,0≤θ＜2π那么除极点外,平面内的点和极坐标就可以了.极角有无数个[3]极坐标与表示同一个点。),())(2,(Zkk一一对应极坐标（，）与平面内的点直角坐标与平面内的点,xy（）一一对应一一对应问题：极坐标与直角坐标都与平面内的点一一对应，即两种坐标系刻画点的本质是一样的，只不过标准不一样，那么能否找到一个桥梁，让这两种坐标进行互化呢？引入新课4352ACBOXDx-6123456-1-2-3-4-5-6-1-2-3-4-51234567OyA'B'C1、探讨极坐标与直角坐标的关系讲授新课x-6123456-1-2-3-4-5-6-1-2-3-4-51234567Oy3542ACBOXD把直角坐标系的原点作为极点，X轴正半轴作为极轴，并且在两种坐标系中取相同的长度单位。互化前提:把直角坐标系的原点作为_____,x轴的正半轴作为_____,并在两种坐标系中取相同的_____极点极轴思考1平面内的一个点的直角坐标是A(1,1),则该点极坐标为______思考2平面内的一个点的极坐标是则该点直角坐标为______)4,2(（0，2）长度单位如图，设点M是平面内任意一点,它的直角坐标是(x,y)，它的极坐标是(ρ,θ)。(x,y)互化前提:把直角坐标系的原点作为极点,x轴的正半轴作为极轴,并且两种坐标系中取相同的长度单位探究新知问题：点M的两种坐标之间有什么关系？任意角的三角函数的定义:),(),,(,22那么其中它与原点的距离是的终边上任意一点角是一个任意角设yxrryxPtan)3(的正切值角cos)2(的余弦值角sin)1(的正弦值角xOry(,)Pxy.知识回顾ryrxxyyxM极坐标M直角坐标(ρ,θ)(x,y)?互化前提:把直角坐标系的原点作为极点,x轴的正半轴作为极轴,并且两种坐标系中取相同的长度单位探究新知sincosyx222tan0xyyxxxOyyxM极坐标与直角坐标的互化关系式:x=ρcosθ,y=ρsinθ通常情况下,将点的直角坐标化为极坐标时,取2,0,0极化直直化极设点M的直角坐标是(x,y)极坐标是(ρ,θ))0(tan,222xxyyx其中角θ的值由该点的象限决定类型一把点的极坐标化为直角坐标例1.将点M的极坐标化成直角坐标.)32,5(思路:利用x=ρcosθ,y=ρsinθ计算讲解例题cos,sin.252535cos,5sin3232553,22xyxy解：由极坐标化成直角坐标的公式：可得：因此，点M的直角坐标为()练习1将点的极坐标化为直角坐标。)4,3(B思路:利用x=ρcosθ,y=ρsinθ计算类型二点的直角坐标化为极坐标化成极坐标的直角坐标将点)1,3(M例23331tan,213)1()3(22xy解：），的极坐标为（点672M67在第三象限，点M22xy第一步：求极径).tan.(:的值定直角坐标所在象限，确再根据该点的先求求极角第二步xy思路：练习2将下列点的直角坐标化为极坐标.22yx第一步：求极径).tan.(:的值定直角坐标所在象限，确再根据该点的先求求极角第二步xy思路：极坐标与直角坐标的互化一.互化前提1.极点和原点重合2.极轴和x轴的正半轴重合3.单位长度一致二.互化公式cossinxy极化直222tan0xyyxx直化极课堂小结