空间向量和垂直关系VIP免费

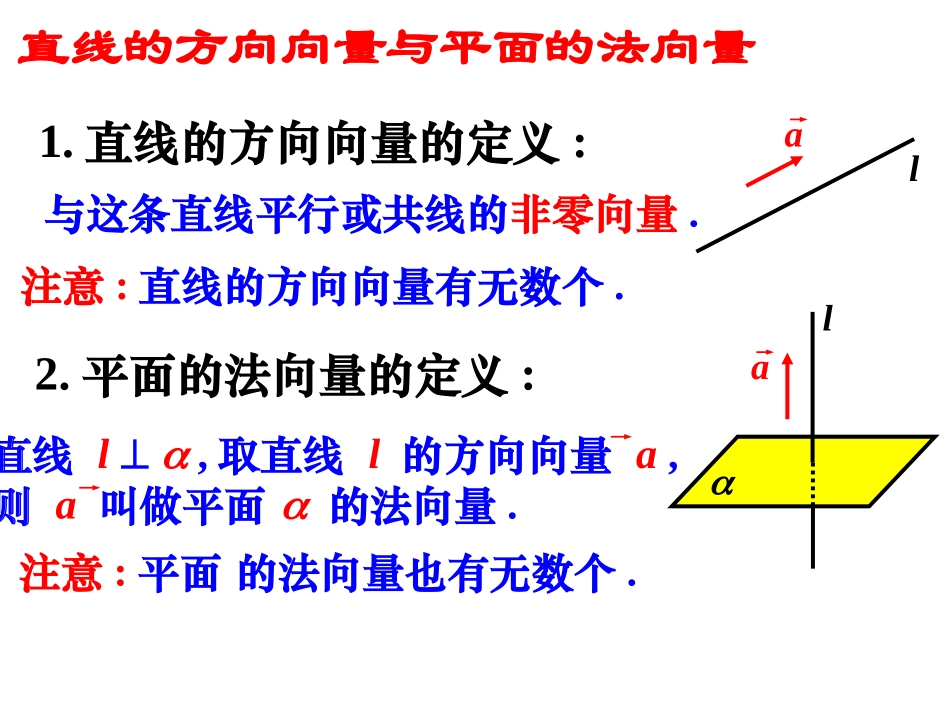
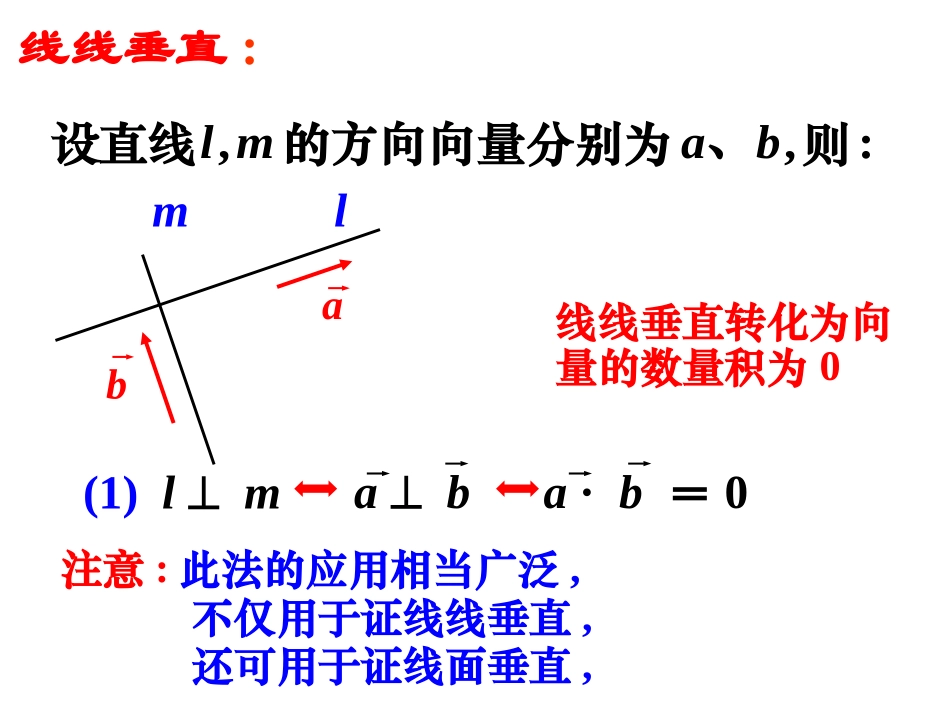
空间向量与垂直关系直线的方向向量与平面的法向量1.直线的方向向量的定义:与这条直线平行或共线的非零向量.2.平面的法向量的定义:注意:直线的方向向量有无数个.直线l,取直线l的方向向量a,则a叫做平面的法向量.laal注意:平面的法向量也有无数个.:,,则、的方向向量分别为设直线baml线线垂直:线线垂直转化为向量的数量积为0mla(1)lmaba·b＝0b注意:此法的应用相当广泛,不仅用于证线线垂直,还可用于证线面垂直,,al的方向向量分别为设直线:,则的法向量分别为平面uADCB线面垂直转化为向量共线线面垂直:aul(2)la∥ua＝u注意:我们一般不用此法证线面垂直,因为求法向量的过程比较复杂.uv:,则、的法向量分别为、平面vu面面垂直转化为向量的数量积为0面面垂直:(3)u⊥vu·v＝0xyz例1.如图,在正方体ABCD－A1B1C1D1中,E,F分别为AB,CC1上的点,AE=CF.求证:A1F⊥B1E.D1知识点一:证明线线垂直ABCDA1C1B1EFG思考:如果不用向量,该如何证明?证明B1E⊥平面A1GFD1.:,1ADBCABCD求证中的正四面体如图在棱长为知识点一:证明线线垂直练习:ADBCxzOyE)0,0,0(D)0,1,0(C),0,21,23(B)36,21,63(A.:,1ADBCABCD求证中的正四面体如图在棱长为yxz知识点一:证明线线垂直练习:ADBCOE)0,33,0(D)36,0,0(A)0,63,21(B)0,63,21(C.,,,,,111111111EFBDMMBBCBBAFEDCBAABCD平面使得上找一点试在棱的中点分别是中在正方体xyz知识点二:证明线面垂直例2.ABCDEFD1A1C1B1M待定系数法:设正方体棱长为1,设点M的坐标为(1,1,z).:,3,,2,1,,90,,0CDAABBABACDACDACDDBADABCDACBABC平面求证之间的距离为与点使点旋转至绕且中已知如图yxz知识点二:证明线面垂直练习:ABCDA')0,21,23(),0,2,0(),2,0,0(),0,0,0(ABCDxyzABCDEMO知识点三:证明面面垂直例3.在四棱锥E－ABCD中,AB⊥平面BCE,CD⊥面BCE,AB＝BC＝CE＝2CD＝2,∠BCE＝120°,求证:平面ADE⊥平面ABE.)2,3,0(),1,0,1(),0,3,0(ADE建系前先证OC,OB,OM两两垂直ACPA变式:在正三棱锥P－ABC中,三条侧棱两两相互垂直,G为△PAB的重心,点E,F分别BC,PB上,BE:EC＝PF:FB＝1:2,求证:平面EFG⊥平面PBC.知识点三:证明面面垂直yzBEFGD设PA＝PB＝PC＝3,则G(1,1,0)F(0,1,0).,,,,,,,3,2,,11111111说明理由若不存在的长求出若存在平面使上是否存在点在线段的中点是形为直角的等腰直角三角底面是以中直三棱柱AFDFBCFFAACADBBACABCCBAABCxyzB1知识点四:利用垂直关系判断存在性例4.BACA1C1FDFC＝FB1＝B1D＝假设存在这样的点F,设点F的坐标为(,0,z),那么2(,,0)2222(－,0,3－z)2(－,,－z)22zyxD1知识点四:利用垂直关系判断存在性变式.如图,正方体ABCD－A1B1C1D1中,E,F分别是BB1,CD的中点.(1)证明:平面AED⊥平面A1FD1;(2)在AE上是否存在一点M,使得A1M⊥平面AED?ABCDA1C1B1EFM假设存在这样的点M,设AM＝AE,则A1M＝A1A＋AM＝A1A＋AE,..3.2.1就用（不建系）向量法好用如果以上两种方法均不标法；或含有动点问题就用坐较繁琐若用性质法较难或过程法；一般情况用传统的性质一般应按以下方式处理在处理线面位置关系时课堂小结0·babalblalBbaba,,mn线线垂直面面垂直线面垂直作业《高效评价训练》P143T11,P144T7,8