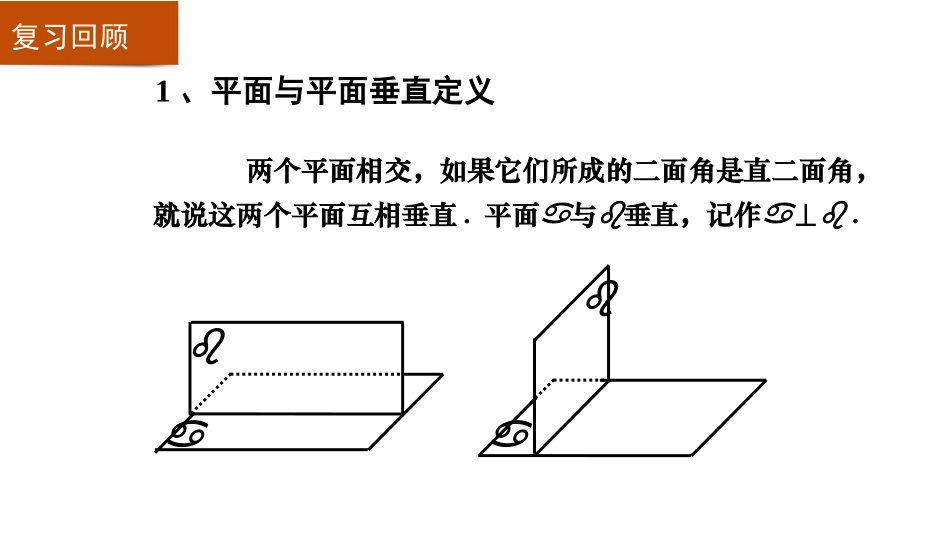
2.3.2平面与平面垂直的判定lll1、平面与平面垂直定义两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.平面与垂直,记作⊥.复习回顾2、利用定义法证明两个平面垂直的步骤:(1)找出或作出二面角的平面角;(2)证明其符合定义(垂直于棱);(3)求出这个角是90。.那么判定两平面互相垂直(面面垂直),除了定义外,还有其他方的判定方法吗?复习回顾问题:观察建筑工地,我们常看到建筑师傅通常用一条系有重物的线(铅垂线)来检测所砌的墙和地面是否垂直,如图所示,建筑师傅只用这样一条线来检测所砌的墙面和地面垂直,可靠吗?这样砌得的墙真的与地面垂直吗?为什么?做模拟小实验铅垂线——模拟铅垂线墙面——书本地面——桌面?结论:问题探究αCDABββE将实际问题转化成数学模型,解释该生活实例中蕴含的数学原理:转化成几何图形铅垂线——直线CD墙面——平面α地面——平面β问题探究如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直βαβαll面面垂直的判定定理符号表示:lABCD线面垂直面面垂直线线垂直获得新知2.如果平面α内有一条直线垂直于平面β内的两条直线,则αβ.⊥()1.如果平面α内有一条直线垂直于平面β内的一条直线,则αβ.⊥()3.如果平面α内的一条直线垂直于平面β内的两条相交直线,则αβ.⊥()一、判断:××√√4.若mα⊥,,则αβ.()⊥m定理的理解1.过平面α的一条垂线可作_____个平面与平面α垂直.2.过一点可作____个平面与已知平面垂直.二、填空题:3.过平面α的一条斜线,可作____个平面与平面α垂直.4.过平面α的一条平行线可作____个平面与α垂直.一无数无数一定理的理解例1如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,求证:平面PAC⊥平面PBC.线线垂直→→面面垂直PABOC定理的应用分析:线面垂直PABOC定理的应用PAα⊥,BC在α内,所以,PABC⊥,因为,点C是圆周上不同于A,B的任意一点,AB为⊙O的直径,所以,BCA∠=90°,即BCCA⊥.又因为PA与AC是△PAC所在面内的两条相交直线,所以,BC⊥平面PAC,又因为BC在平面PBC内,所以平面PAC⊥平面PBC.证明:设⊙O所在平面为α,由已知条件,已知ABCD是正方形,O是正方形的中心,PO⊥平面ABCD,E是PC的中点,求证:平面PAC⊥平面BDE.定理的应用跟踪训练1因为PO⊥平面ABCD,则可知CO、AO分别是所以BDPC,BDPA;⊥⊥又PA,PB都在平面PAC中,且相交,BD⊥平面PAC,又BD在平面BDE中.BDPACOEPC和PA在平面ABCD中的射影,又知正方形ABCD,则有COBD⊥、AOBD.⊥证明:ABCD在四面体ABCD中,BD=2,AB=AD=CB=CD=AC=1,求证:平面ABD⊥平面BCD.ABCDO定理的应用跟踪训练2线线垂直→→面面垂直分析:线面垂直思路一:两平面的二面角是直二面角思路二:ABCDO在四面体ABCD中,BD=2,AB=AD=CB=CD=AC=1,求证:平面ABD⊥平面BCD.ABCDO定理的应用跟踪训练2取BD的中点为O,连接AO、CO.又因为ΔAOC中,有,COAOAC2221故在RtΔABO和RtΔBCO中,BO=,22因为AB=AD=1、CB=CB=1,所以AOBD⊥、COBD;⊥22所以AO=OC=所以AOCO;⊥证明:又CO、BD都在平面BCD,且交于点O所以AO⊥平面BCD;又因为AO在平面ABD中,从而得到平面ABD⊥平面BCD(1)利用定义;(2)利用判定定理.即2.数学思想方法:转化的思想空间问题平面问题1.判定面面垂直的两种方法:面面垂直证明两平面所成的二面角为直二面角βαβαll知识小结线面垂直线线垂直学法P117-118那么如果在已知这些面面垂直的条件下,又能得到哪些结论?课后探究及作业课后探究课后作业,CDBCBCDAB,面已知请问哪些平面是互相垂直的,为什么?ABCD,CDBCBCDAB,面已知请问哪些平面是互相垂直的,为什么?ABCD定理的应用跟踪训练2因为AB⊥面BCD,AB在平面ABC和平面ABD,则有平面ABD⊥平面BCD、平面ABC⊥平面BCD;由AB⊥面BCD,可知ABCD;⊥又BCCD⊥,且BC是AC在平面BCD内的射影,可得CD⊥平面ABC;又因为CD在平面ACD中,所以平面ACD⊥平面ABC.解: