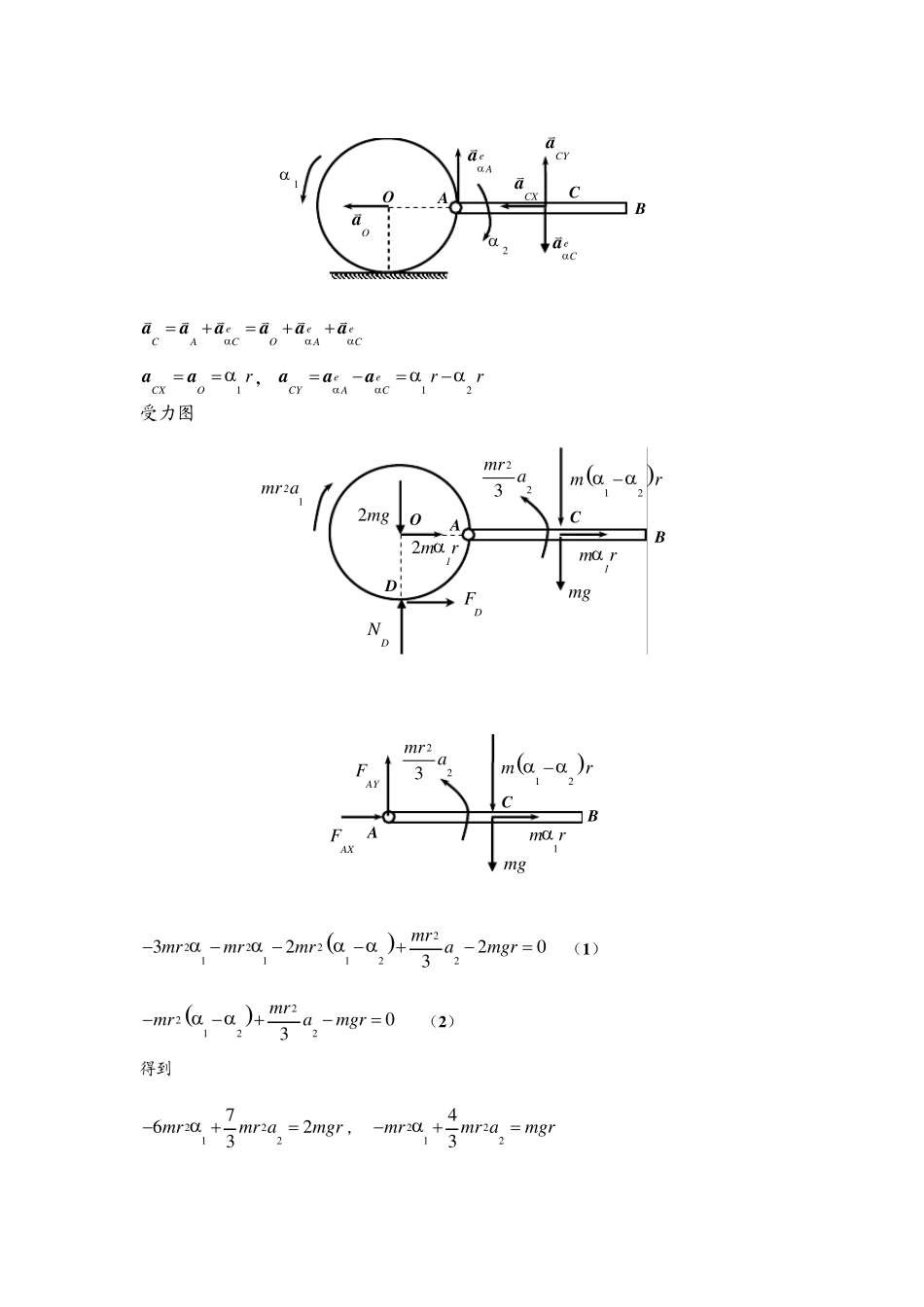
理论力学期终考试试卷(A ) (机动学院 05-06 学年)2005.12.1 1.曲柄连杆滑块机构如图所示。曲柄OD 长2l,与长为l 的连杆AB 用铰链连接,铰点A 为OD 的中点。在OD 的E 处作用铅垂向下、大小为F 的力,/ 2AEl=;在滑块B 上作用水平向左、大小为F 的力;在连杆AB 上作用顺时针、大小为M 的力偶。不计各构件的重力,用虚位移原理求系统平衡时 M 和 F 之间的关系。 OABFF Mθ θ E 用虚位移原理 0EBF yF xMδδδθ−−+= 3 sin2Elyθ=, 3 cos2Elyδθ δθ= 2 cosBxlθ=, 2 sinBxlδθ δθ= − 3 cos2 sin02lFF lMθ δθθ δθδθ−++= 得到平衡条件为 3 cos2 sin02lFF lMθθ−++= DI ω ω vAvBvCC 2.长为l 的匀质杆OA,AB 和长为2l / 3 的匀质杆BD 用铰链连接,如图所示。OA,BD,AB 的质量均为m。碰撞前系统静止,在 OA 的中点处作用水平的冲量 I,求碰撞后杆OA,AB 和BD 的角速度 解:运动学分析 OAωω= AB 作瞬时平动,0ABω=,32 /32 /32BABDvvllωω=== O A BI B DA IAX IAY IOY IOX IAX IAY IBXIBYIBY IBXIDX IDY 2132AXI lmlIlω =− (1 ), AXBXm lIIω =− (2 ) 212323323BXmlIlω⎛⎞=⎜⎟⎝⎠ (3 ), AYBYOII=+ (4 ) 22AYBYllOII=− (5 ) (1)+(2)× l +(3)×3 / 2 : 2532I lml ω =, 得到 310Imlω =, 310OAImlωω==, 39220BDImlωω==, 0ABω= 3.一长为2r,质量为m 的杆,一端铰接于圆轮轮缘上一点 A,圆轮放在一粗糙的水平面上,如图所示。设圆轮的质量为2m,半径为r,可以看作匀质圆盘。图示位置 AB 水平,系统无初速地开始运动,用达朗贝尔原理求此时轮心的加速度和杆AB 的角加速度。 解:运动学分析 O ABg OABα 1 α 2 eAαaveCαavCOav CXavCYav eeeCACOACααα=+=++aaaaaavvvvvv 1CXOrα==aa, 12eeCYACrrαααα=−=−aaa 受力图 OAB C()12mrαα− 12mra 21mrαmg223mr aD2 mgDNDF1mrα A BC1mrα()12mrαα−mg223mr aAXF AYF ()22221112232203mrmrmrmramgrαααα−−−−+−= (1 ) ()2212203mrmramgrαα−−+−= (2 ) 得到 22127623mrmramgrα−+=, 221243mrmramgrα−+= 221743 mr amgr=,21217gar=,14 12163 171717gggggarrrrr=⋅−=−= − 4.如图所示,长为l,质量为m 的杆AB 的A端与质量为m 的...