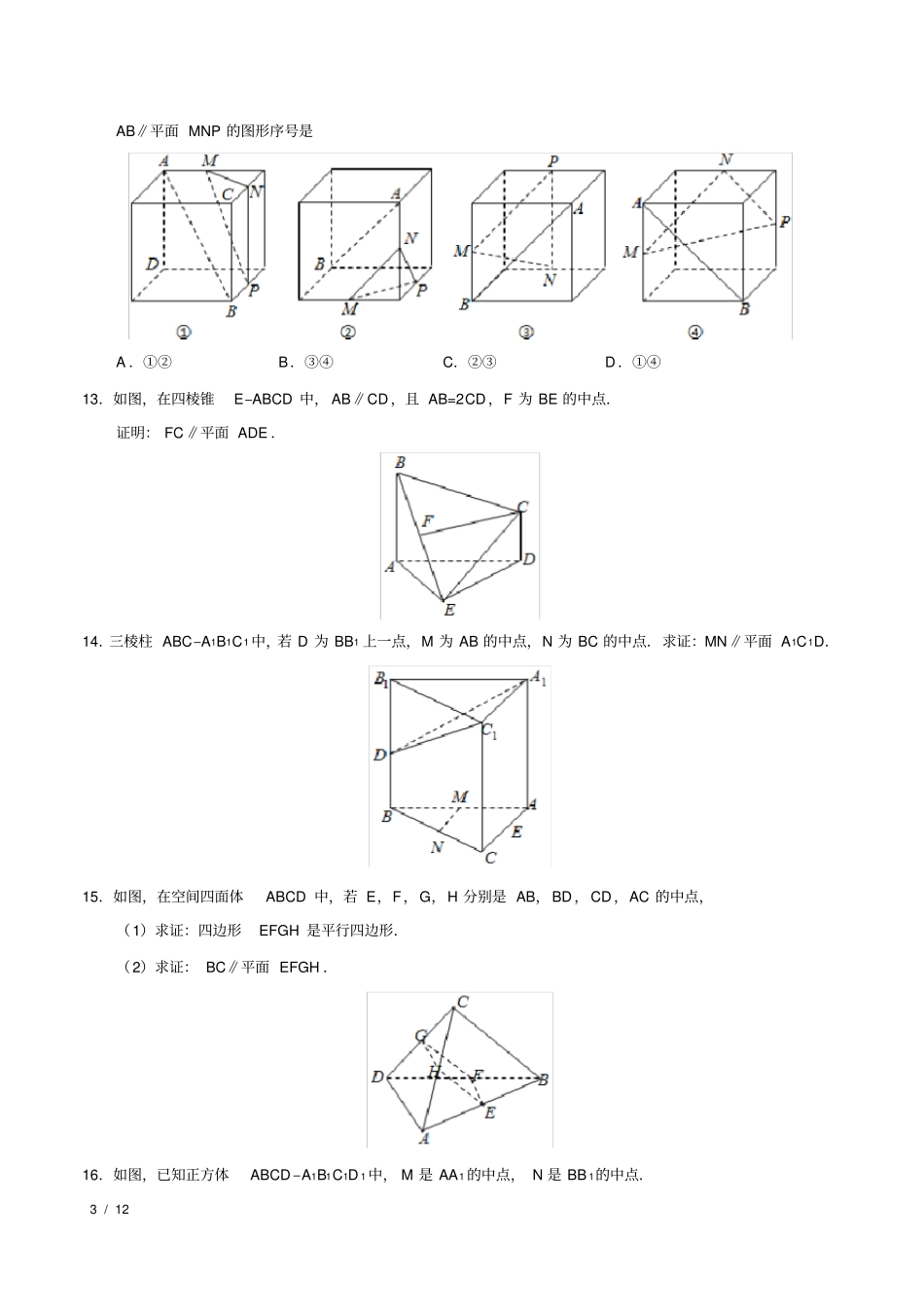
1 / 12基础训练1.A,b, c 为三条不重合的直线,α,β,γ 为三个不重合平面,现给出六个命题①? a∥b,②? a∥b,③? α∥β,④? α∥β,⑤? α∥a,⑥? α∥ a,其中正确的命题是A .①②③B.①④⑤C.①④D.①③④2.在正方体ABCD –A1B1C1D 1 中,与平面ACC1A1 平行的棱共有A .2 条B.3 条C.4 条D.6 条3.已知直线a,b,平面 α,满足 a? α,则使 b∥α 的条件为A .b∥aB.b∥a 且 b?αC. a 与 b 异面D. a 与 b 不相交4.如图,四棱锥P–ABCD 中, M,N 分别为 AC, PC 上的点,且MN∥平面 PAD,则A .MN∥ PDB.MN ∥PAC. MN∥ADD.以上均有可能5.直线 m 与平面 α 平行的充要条件是A .直线 m 与平面 α 没有公共点B.直线 m 与平面 α 内的一条直线平行C.直线 m 与平面 α 内的无数条直线平行D.直线 m 与平面 α 内的任意一条直线平行6.平面 α 与平面 β 平行的条件可以是A .α 内有无穷多条直线与β 平行B. α 内的任何直线都与β 平行C.直线 a 在平面 α 内,直线 b 在平面 β 内,且 a∥β,b∥αacbcabcccaca2 / 12D.直线 a∥α,直线 a∥β7.下列条件中,能得到两个平面平行的条件是A .有一条直线与这两个平面都平行B.有两条直线与这两个平面都平行C.有一条直线与这两个平面都垂直D.有一条直线与这两个平面所成的角相等8.如图所示,三棱柱ABC–A1B1C1,D 是 BC 的中点, D1 是 B1C1 的中点.求证:(1)A1B∥平面 AC1D;(2)平面 A1BD1∥平面 AC1D.9.如图,在四棱锥P–ABCD 中, PD ⊥平面 ABCD ,底面 ABCD 为菱形,.点分E,F,G,H 别是棱 AB,CD ,PC,PB 上共面的四点,且BC∥EF.证明: GH ∥EF.能力提升10.下列四个命题中,不正确的是A .若平面内有两条相交直线与平面内的两条相交直线分别平行,则两个平面平行B.平行于同一平面的两个平面平行C.如果平面内有无数条直线都与平面平行,则两个平面平行D.如果平面内任意一条直线都与平面平行,则两个平面平行11.过三棱柱ABC–A1B1C1 的任意两条棱的中点作直线,其中与平面ABB1A1 平行的直线共有A .4 条B.6 条C.8 条D.12 条12.如图,下列四个正方体图形中,A、B 为正方体的两个顶点,M、N、P 分别为其所在棱的中点,能得出3 / 12AB∥平面 MNP 的图形序号是A .①②B.③④C.②③D.①④13.如...