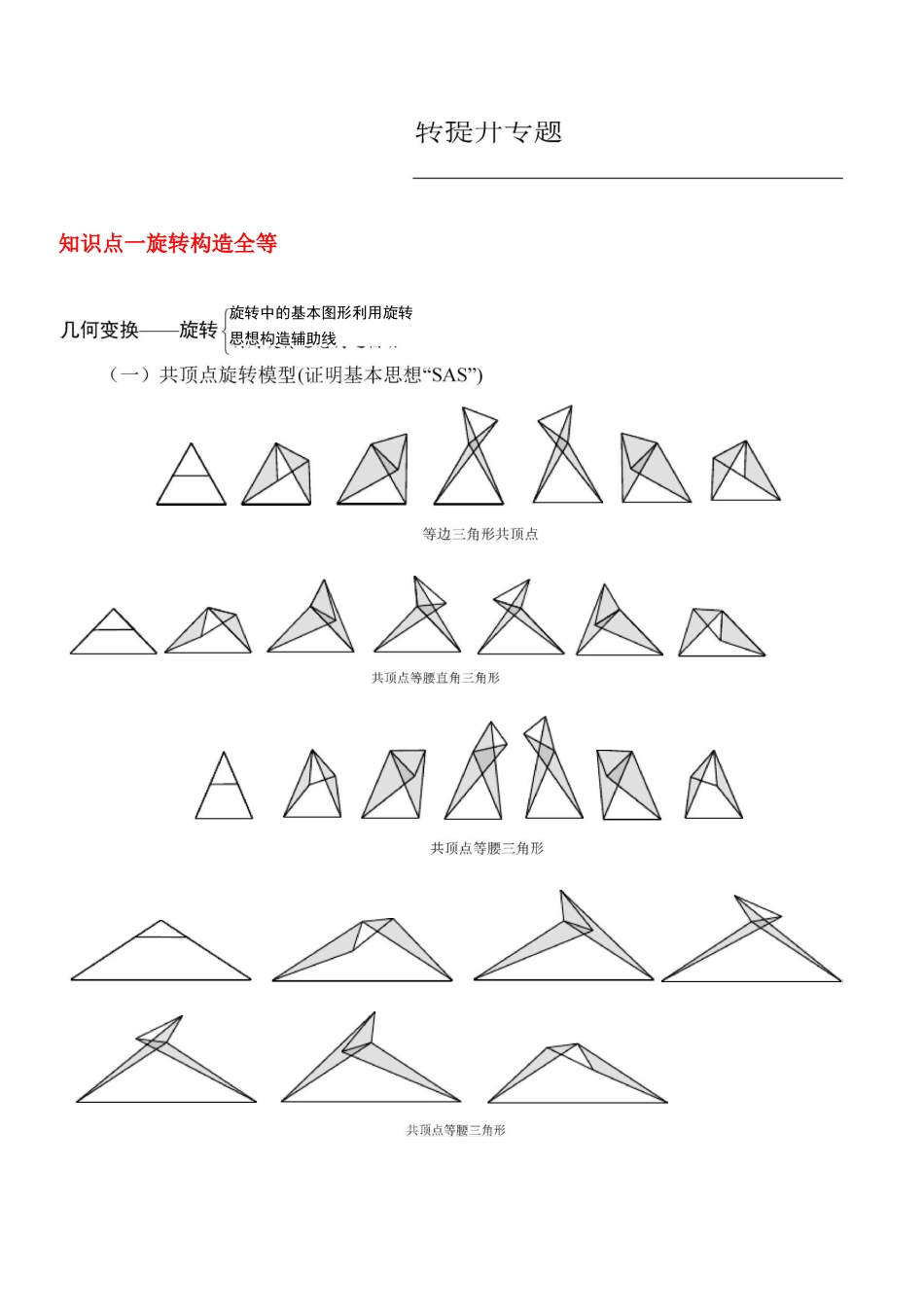
知识点一旋转构造全等旋转中的基本图形利用旋转思想构造辅助线以上给出了各种图形连续变化图形,图中出现的两个阴影部分的三角形是全等三角形,此模型需要注意的是利用“全等三角形”的性质进行边与角的转化二利用旋转思想构造辅助线(1) 根据相等的边先找出被旋转的三角形(2) 根据对应边找出旋转角度(3) 根据旋转角度画出对应的旋转的三角形三旋转变换前后具有以下性质:(1) 对应线段相等,对应角相等(2) 对应点位置的排列次序相同(3) 任意两条对应线段所在直线的夹角都等于旋转角 0.【例题精讲】例 1•在四边形 ABCD 中,zADC 二 zABC=90。,AD 二 CD,DP 丄 AB 于 P,若 S^=25,求ABCDDP 的长。例 2•如图,四边形 ABCD 是正方形,AABE 是等边三角形,M 为对角线 BD 上任意一点,将 BM绕点 B 逆时针旋转 60°得到 BN,连接 AM、CM、EN-⑴ 求证:AAMB9AENB⑵① 当 M 点在何处时,AM+CM 的值最小;② 当 M 点在何处时,AM+BM+CM 的值最小,并说明理由;⑶ 当 AM+BM+CM 的最小值为+1 时,求正方形的边长.方法总结:1、共顶点的等线段中,最常用旋转思路,但也不可以思维定势,辅助线叙述中用一般语言2、旋转变换还用于处理:① 几何最值问题:几何最值两个重要公理依据是:两点之间线段最短和垂线段最短;② 有关线段的不等关系;③ 自己构造绕某点旋转某角度(特别是 60 度),把共顶点的几条线段变为首尾相接的几条线段,再变为共线取得最小值问题,计算中常用到等腰三角形或勾股定理等知识。【课堂练习】1•如图 1 已知边长为 a的正方形 ABCD和边长为 b的正方形 AEFG 有一个公共点 A,(a>2b),且点 F在 AD 上。(以下结果可以用含 a、b的代数式表示)⑴ 求 LDBF;(2)把正方形 AEFG 绕点 A逆时针旋转 45°,得到图 2,求图 2 中的 S&曰曰(3)把正方形 AEFG 绕点 A旋转任意角度,在旋转的过程中,S^DBF是否存在最大值、最小值?如果存在,试求出最大值、最小值;若不存在,请说明理由。2•四边形 ABCD中,乙 DAB=乙 BCD=90°,CD=CB,AC=P3,求四边形 ABCD 的面积。C图C图AADFCBEEAC1,求知识点三(知识点名称)【例题精例如图,“BC 中,AB=AC=1rzBAC=454,丄址涯由皿眈堤静尉赃时方向虚转潯到的,连接 BE、CF®交于点 D,⑴ 喩证:BE=CF;(2)当四边形垃 DE 为萋形时「求 BD 的懐・£虻圄.MB 匚口 P±汕「=$『.如 E 匸=4 宁.AB=2^.D 昙叢段 B「上时—t■副...