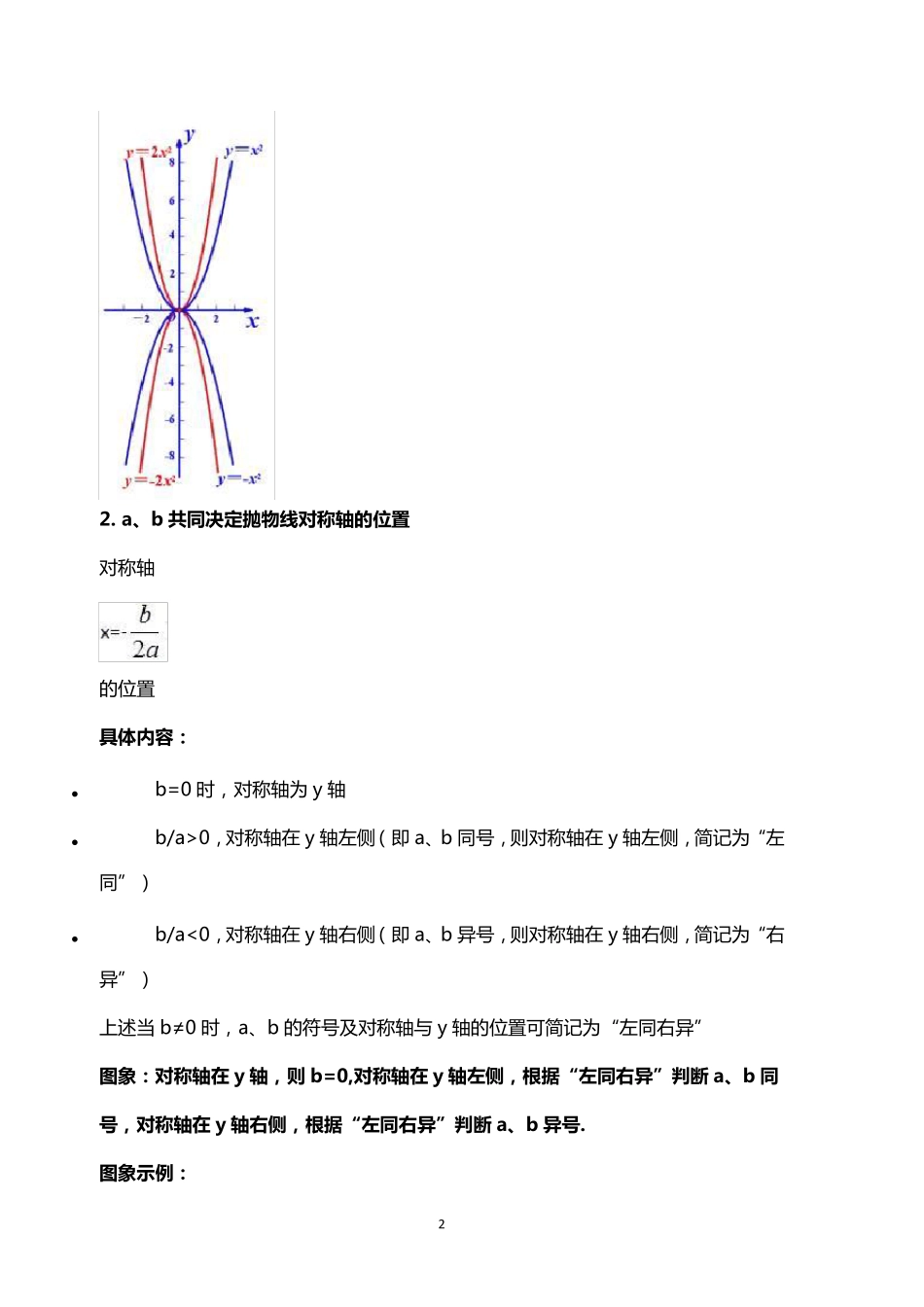
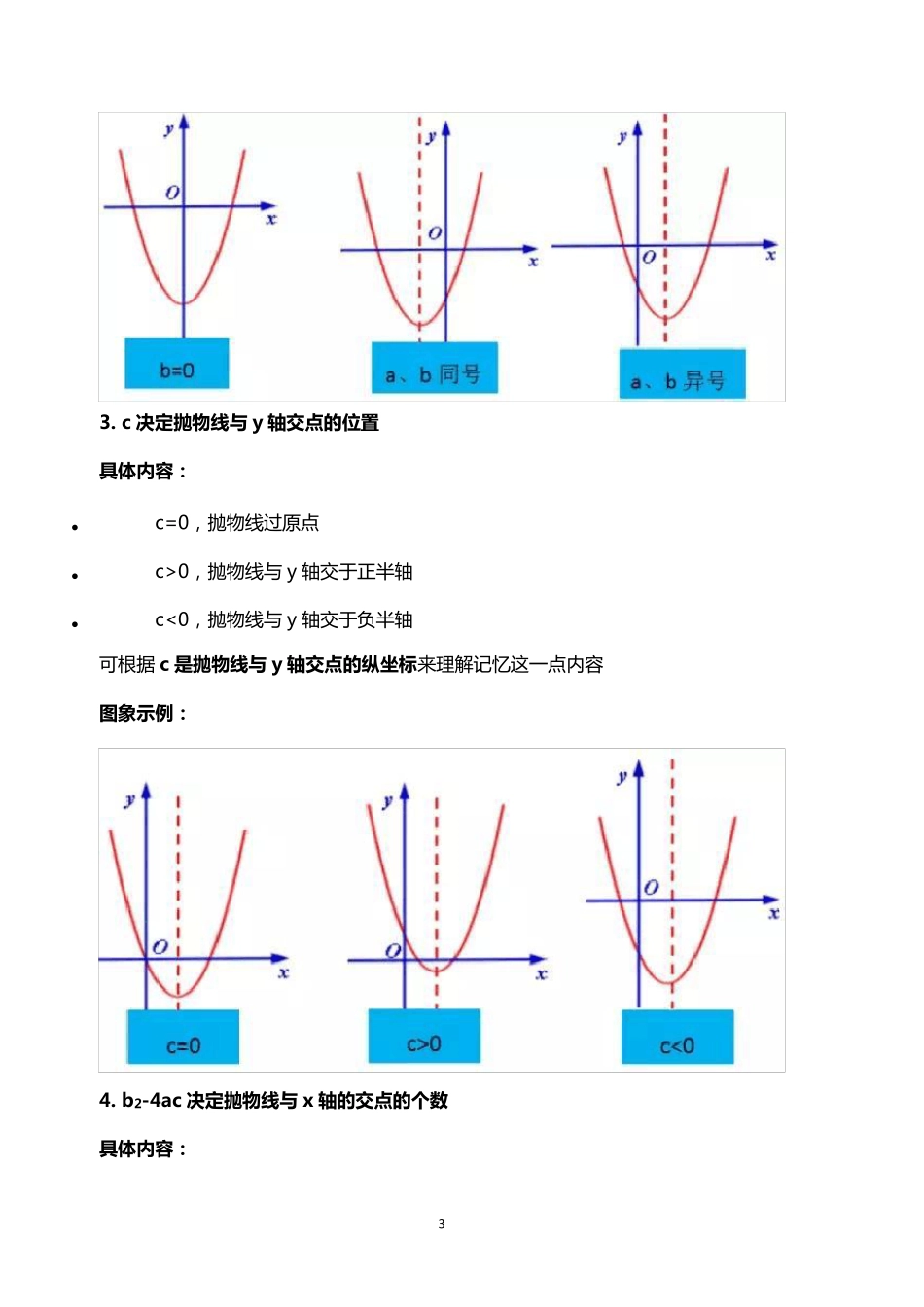
1 二次函数图象与系数的关系最全总结 二 次 函 数 是 初 中 数 学 的 重 点 也 是 难 点 内 容 之 一 ,它 的 图 象 是 一 条 抛 物 线 ,其 形 状 、开口方向、位置等与表达式中的系数的关系非常密切。 所 以 , 二 次 函 数 图 象 与 a、b、c 的 关系是 非常重 要的 一 个知识点 , 今天, 小培就为大家总结一 下二 次 函 数 图 像与 系数 的 关系变化。 1. a 决定抛物线的开口方向及大小 具体内容: • a>0, 抛 物 线 开口向上 • a<0, 抛 物 线 开口向下 • |a|越大, 抛 物 线 的 开口越小 • |a|越小, 抛 物 线 的 开口越大 我们知道抛物线平移前后形 状 及开口方向不变,只是位置发生改变, 那么只要两个二次 函 数 的a 相同, 那么就可以 由其中 一 个二 次 函 数 通过平移得到另一 个二 次 函 数. 图象:抛物线开口向上,a>0,抛物线开口向下,a<0,开口大的抛物线的|a|小于开口小的抛物线的|a|. 图象示例: 2 2. a、 b 共 同 决 定 抛 物 线 对 称 轴 的 位 置 对 称 轴 的 位 置 具 体 内 容 : • b=0 时 , 对 称 轴 为 y 轴 • b/a>0, 对 称 轴 在 y 轴 左 侧 ( 即 a、b 同 号 , 则 对 称 轴 在 y 轴 左 侧 , 简 记 为 “左同 ”) • b/a<0, 对 称 轴 在 y 轴 右 侧 ( 即 a、b 异 号 , 则 对 称 轴 在 y 轴 右 侧 , 简 记 为 “右异 ”) 上 述 当 b≠0 时 , a、b 的 符 号 及 对 称 轴 与 y 轴 的 位 置 可 简 记 为 “左 同 右 异 ” 图 象 : 对 称 轴 在 y 轴 , 则 b=0,对 称 轴 在 y 轴 左 侧 , 根 据 “左 同 右异”判断 a、 b 同号, 对 称 轴 在 y 轴 右侧 , 根 据 “左 同 右异”判断 a、 b 异号. 图 象 示例: 3 3. c 决 定 抛 物 线 与 y 轴交点的位置 具体内容: • c=0, 抛 物 线 过 原 点 • c>0, 抛 物 线 与 y 轴 交 于 正 半 轴 • c<0, 抛 物 线 与 y 轴 交 于 负 半 轴 可 根 据 c 是抛 物 线 与 y 轴交点的纵坐标来 理 解 记 忆 这 一点 内容 图象示例: 4. b2-4ac 决 定 抛 物 线 与 x 轴的交点的...