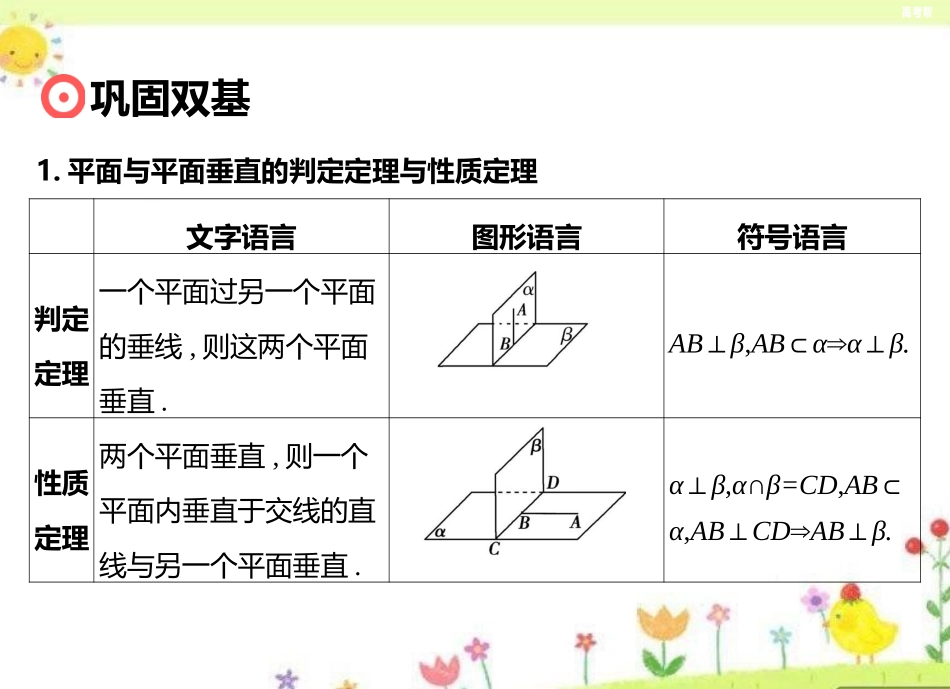
立体几何中的面面垂直本节主要包括知识点:1.平面与平面垂直的判定与性质2.平面图形的翻折问题开门见山文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线,则这两个平面垂直.AB⊥β,AB⊂α⇒α⊥β.性质定理两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.α⊥β,α∩β=CD,AB⊂α,AB⊥CD⇒AB⊥β.1.平面与平面垂直的判定定理与性质定理巩固双基2.二面角(1)二面角的平面角:如图,在二面角α-l-β的棱l上任取一点P,以点P为垂足,在半平面α,β内分别作垂直于棱l的射线PA和PB,则射线PA和PB构成的∠APB叫作二面角α-l-β的平面角.二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度.我们规定,二面角的取值范围是[0°,180°].平面角是直角的二面角叫作直二面角.(2)找二面角的平面角的方法①垂面法:由二面角的平面角的定义知,只需作与棱垂直的平面,则该平面与两个半平面的交线构成的角即二面角的平面角.②定义法:先分别在两个半平面内找一条垂直于棱的射线,然后平移到一起,两射线的夹角即二面角的平面角.面面垂直的判定与性质【例1】(2018·全国卷Ⅰ)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°.以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.(1)证明:平面ACD⊥平面ABC;(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ=23DA,求三棱锥QABP的体积.典型例题1[解](1)证明:由已知可得,∠BAC=90°,BA⊥AC.又BA⊥AD,且AC⊂平面ACD,AD⊂平面ACD,AC∩AD=A,所以AB⊥平面ACD.又AB⊂平面ABC,所以平面ACD⊥平面ABC.(2)由已知可得,DC=CM=AB=3,DA=32.又BP=DQ=23DA,所以BP=22.作QE⊥AC,垂足为E,则QE13DC.由已知及(1)可得DC⊥平面ABC,所以QE⊥平面ABC,QE=1.因此,三棱锥QABP的体积为VQ-ABP=13×QE×S△ABP=13×1×12×3×22sin45°=1.证明面面垂直的2种方法(1)定义法:利用面面垂直的定义,即判定两平面所成的二面角为直二面角,将证明面面垂直问题转化为证明平面角为直角的问题.(2)定理法:利用面面垂直的判定定理,即证明其中一个平面经过另一个平面的一条垂线,把问题转化成证明线线垂直加以解决,注意:三种垂直关系的转化规律方法(2018·江苏高考)在平行六面体ABCDA1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.小试牛刀(2018·江苏高考)在平行六面体ABCDA1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.[证明](1)在平行六面体ABCDA1B1C1D1中,AB∥A1B1.因为AB⊄平面A1B1C,A1B1⊂平面A1B1C,所以AB∥平面A1B1C.小试牛刀(2)在平行六面体ABCDA1B1C1D1中,四边形ABB1A1为平行四边形.又因为AA1=AB,所以四边形ABB1A1为菱形,因此AB1⊥A1B.又因为AB1⊥B1C1,BC∥B1C1,所以AB1⊥BC.又因为A1B∩BC=B,A1B⊂平面A1BC,BC⊂平面A1BC,所以AB1⊥平面A1BC.因为AB1⊂平面ABB1A1,所以平面ABB1A1⊥平面A1BC.平面图形的翻折问题【例2】如图1,在直角梯形ABCD中,AD∥BC,∠BAD=π2,AB=BC=12AD=a,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图2中△A1BE的位置,得到四棱锥A1BCDE.2典型例题(1)证明:CD⊥平面A1OC;(2)当平面A1BE⊥平面BCDE时,四棱锥A1BCDE的体积为362,求a的值.图1图2[解](1)证明:在题图1中,连接EC(图略),因为AB=BC=12AD=a,E是AD的中点,∠BAD=π2,所以BE⊥AC.即在题图2中,BE⊥A1O,BE⊥OC,从而BE⊥平面A1OC.又CD∥BE,所以CD⊥平面A1OC.(2)由已知,平面A1BE⊥平面BCDE,且平面A1BE∩平面BCDE=BE,又由(1)可得A1O⊥BE,所以A1O⊥平面BCDE.即A1O是四棱锥A1BCDE的高.由题图1知,A1O=AO=22AB=22a,平行四边形BCDE的面积S=BC·AB=a2,从而四棱锥A1BCDE的体积为V=13S·A1O=13×a2×22a=26a3.由26a3=362,得a=6.平面图形的翻折问题,关键是搞清翻折前后图形中线面位置关系和度量关系的变化情况.一般地,翻折后还在同一平面上的性质不发生变化,不在同一个平面上的性质发生变化.规律方法(2018·鄂州模拟)如图,在Rt△ABC中,AB=BC=3,点E,F分别在线段AB,AC上,且EF∥BC,将...