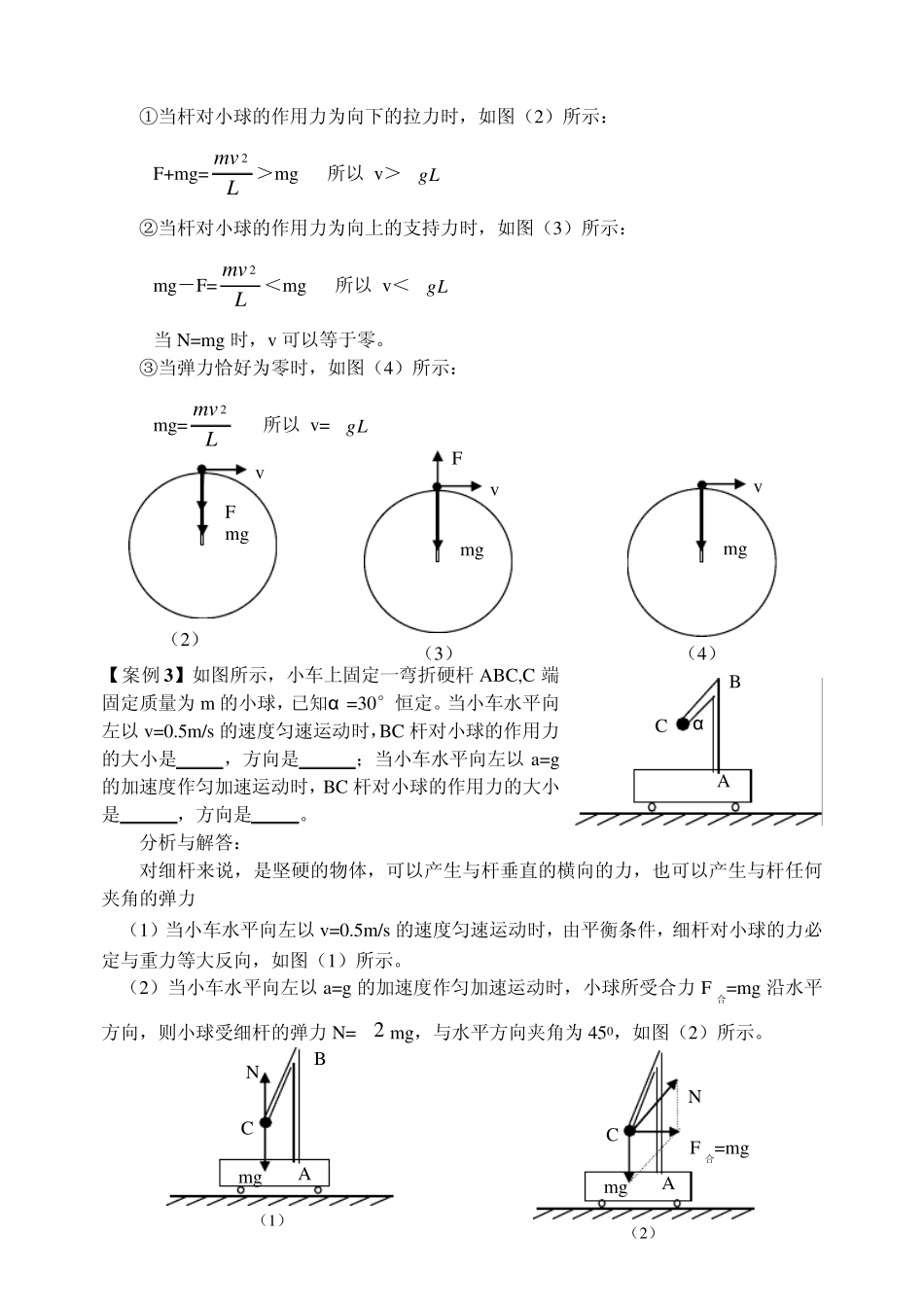
案例1 绳子、弹簧和杆产生的弹力特点 模型特点: 1. 轻绳 (1)轻绳模型的特点 “绳”在物理学上是个绝对柔软的物体,它只产生拉力(张力),绳的拉力沿着绳的方向并指向绳的收缩方向。它不能产生支持作用。 它的质量可忽略不计,轻绳是软的,不能产生侧向力,只能产生沿着绳子方向的力。它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长。 (2)轻绳模型的规律 ①轻绳各处受力相等,且拉力方向沿着绳子; ②轻绳不能伸长; ③用轻绳连接的系统通过轻绳的碰撞、撞击时,系统的机械能有损失; ④轻绳的弹力会发生突变。 2. 轻杆 (l)轻杆模型的特点 轻杆的质量可忽略不计,轻杆是硬的,能产生侧向力,它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长或压缩。 (2)轻杆模型的规律 ①轻杆各处受力相等,其力的方向不一定沿着杆的方向; ②轻杆不能伸长或压缩; ③轻杆受到的弹力的方式有拉力或压力。 3. 轻弹簧 (1)轻弹簧模型的特点 轻弹簧可以被压缩或拉伸,其弹力的大小与弹簧的伸长量或缩短量有关。 (2)轻弹簧的规律 ①轻弹簧各处受力相等,其方向与弹簧形变的方向相反; ②弹力的大小为 F=kx,其中 k 为弹簧的劲度系数,x为弹簧的伸长量或缩短量; ③弹簧的弹力不会发生突变。 案例探究: 【案例 1】如图所示,一质量为 m 的物体系于长度分别为 L1、L2 的两根细绳OA、OB 上,0B 一端悬挂在天花板上,与竖直方向夹角为θ ,OA 水平拉直,物体处于平衡状态,现在将 OA 剪断,求剪断瞬间物体的加速度,若将绳OB 换为长度为 L2 的弹簧,结果又如何? O B A θ O B A 分析与解答: 为研究方便,我们两种情况对比分析。 (1)剪断前,两种情况小球受力一样,分别如图(1)、(2)所示,利用平衡条件,则 mg 与F2 的合力与F1 大小相等,方向相反,可以解得 F1=mgtgθ 。 (2)剪断后瞬间,绳 OA 产生的拉力F1 消失, 对绳来说,其伸长量很微小,可以忽略不计,不需要形变恢复时间,因此,绳子中的张力也立即发生变化,这时 F2 将发生瞬时变化,mg 与F2 的合力将不再沿水平方向,而是由于小球下一时刻做单摆运动沿圆弧的切线方向,与绳垂直,如图(3)所示,F合=mgsinθ ,所以 a=gsinθ 。 对弹簧来说,其伸长量大,形变恢复需要较长时间,认为弹簧的长度还没有发生变化。这时 F2 不发生变化,故 mg 与F2 的合力仍然保持不变,...