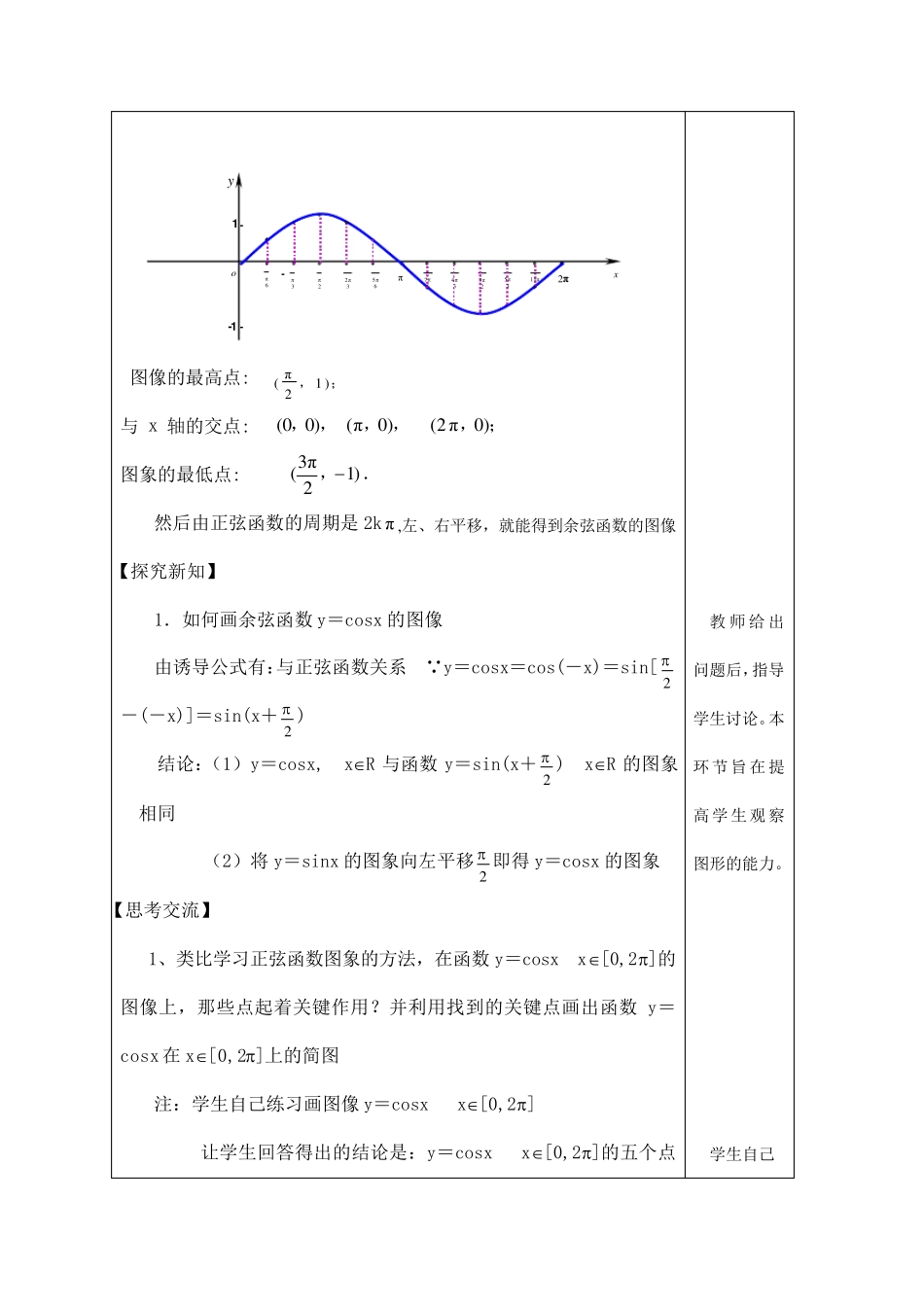
《余弦函数的图像与性质》第一课时教学设计 陕西省丹凤中学 李胜红 一、教学目标: 1、知识与技能 (1)能画出余弦函数在[ 0,2 ]的图像;(2)熟练根据余弦函数的图像推导出余弦函数的性质;(3)掌握利用数形结合思想分析问题、解决问题的技能。 2、过程与方法 能学以致用,尝试用五点作图法作出余弦函数的图像,并能结合图像分析得到余弦函数的性质;且能简单的应用余弦函数的性质。 3、情感态度与价值观 让学生体验自身探索成功的喜悦感,培养学生的自信心;使学生认识到转化“矛盾”是解决问题的有效途经;培养学生形成实事求是的科学态度和锲而不舍的钻研精神。 二、教学重、难点 重点:由余弦函数的图像总结出余弦函数的性质,且能简单的应用余弦函数的性质 难点: 余弦函数性质的应用。 三、教学方法法:合作交流式 四、教学过程 【复习回顾】 (1)五点法作正弦函数的图像y = sin x ,x R 教师提问,让学生回答; 图像的最高点: 与 x 轴的交点: 图象的最低点: 然后由正弦函数的周期是2k π ,左、右平移,就能得到余弦函数的图像 【探究新知】 1.如何画余弦函数y=cosx 的图像 由诱导公式有:与正弦函数关系 y=cosx=cos(-x)=sin[2-(-x)]=sin(x+2 ) 结论:(1)y=cosx, xR 与函数y=sin(x+2 ) xR 的图象相同 (2)将 y=sinx 的图象向左平移2 即得y=cosx 的图象 【思考交流】 1、类比学习正弦函数图象的方法,在函数y=cosx x[0,2]的图像上,那些点起着关键作用?并利用找到的关键点画出函数y=cosx 在 x[0,2]上的简图 注:学生自己练习画图像y=cosx x[0,2] 让学生回答得出的结论是:y=cosx x[0,2]的五个点 教 师 给 出问题后,指导学生讨论。本环节旨在提高学生观察图形的能力。 学生自己π(1 )2 ,;(00 ),,(2 π0 ),;(π0 ),,3 π(1 )2,.2 oxy- - -1 1 - π3π22 π35 π6π764 π33 π25 π31 1 π6ππ6关键是(0,1) (2 ,0) (,-1) (23 ,0) (2,1) 2、观察函数y=cosx,x∈R 的图像,总结余弦函数的的性质 观察上图可以得到余弦函数y=cosx 有以下性质:(学生回答教师讲解并完成表格) (1)定义域:y=cosx 的定义域为R (2)值域: y=cosx 的值域为[-1,1],即有 |cosx|≤1(有界性) (3)最值:1对于y=cosx 当且仅当x=2k,kZ 时 ymax=1 当且...