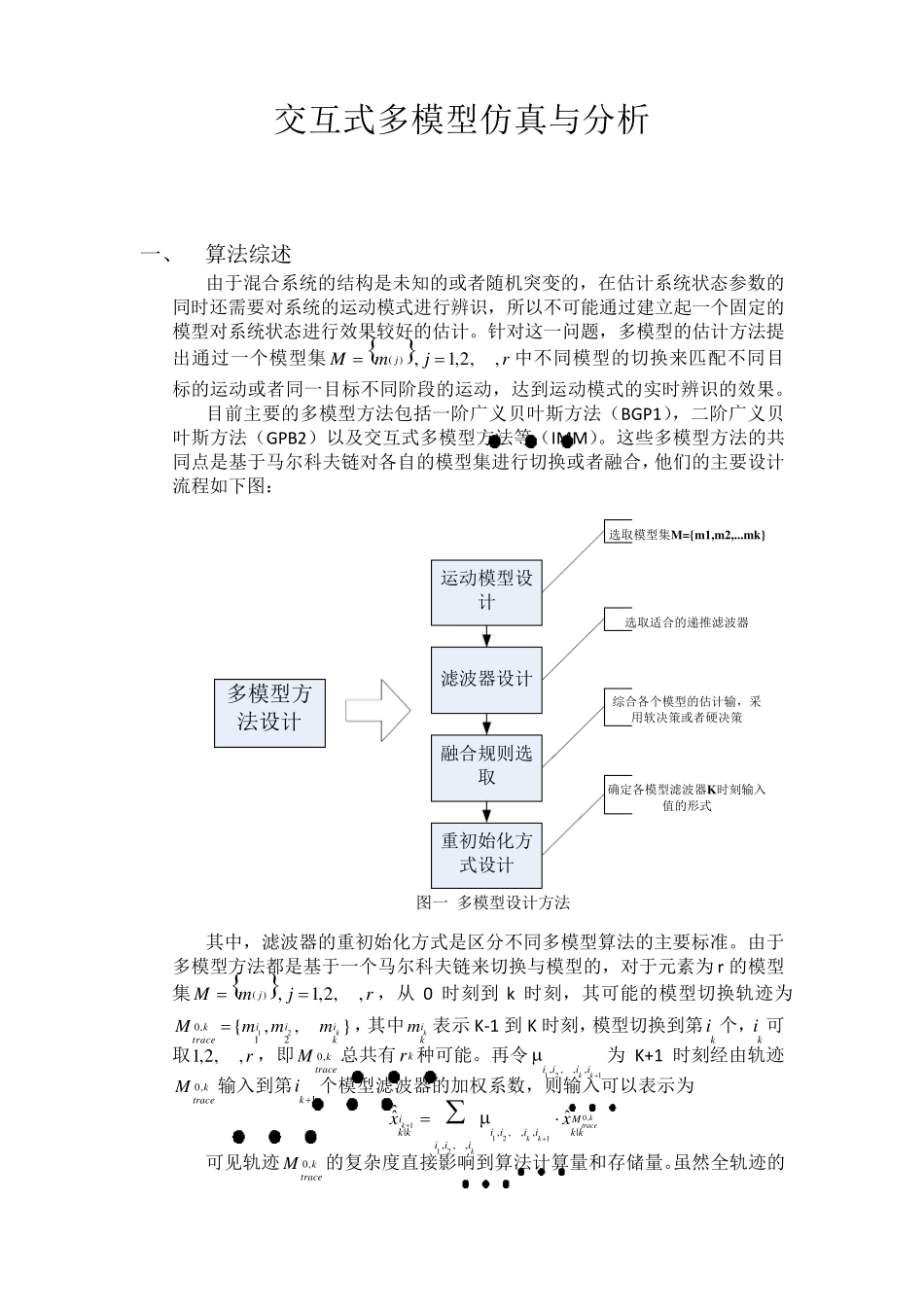
硕0 3 7 班 刘文 3 1 1 0 0 3 8 0 2 0 2 0 1 1 / 4 / 2 0 交互式多模型仿真与分析 IMM 算法与 GBP算法的比较,算法实现和运动目标跟踪仿真,IMM 算法的特性分析 交互式多模型仿真与分析 一、 算法综述 由于混合系统的结构是未知的或者随机突变的,在估计系统状态参数的同时还需要对系统的运动模式进行辨识,所以不可能通过建立起一个固定的模型对系统状态进行效果较好的估计。针对这一问题,多模型的估计方法提出通过一个模型集( ) ,1,2,,jMmjr中不同模型的切换来匹配不同目标的运动或者同一目标不同阶段的运动,达到运动模式的实时辨识的效果。 目前主要的多模型方法包括一阶广义贝叶斯方法(BGP1),二阶广义贝叶斯方法(GPB2)以及交互式多模型方法等(IMM)。这些多模型方法的共同点是基于马尔科夫链对各自的模型集进行切换或者融合,他们的主要设计流程如下图: 运动模型设计滤波器设计融合规则选取重初始化方式设计选取模型集M={m1,m2,...mk}选取适合的递推滤波器综合各个模型的估计输,采用软决策或者硬决策确定各模型滤波器K时刻输入值的形式多模型方法设计 图一 多模型设计方法 其中,滤波器的重初始化方式是区分不同多模型算法的主要标准。由于多模型方法都是基于一个马尔科夫链来切换与模型的,对于元素 为 r 的模型集( ) ,1,2,,jMmjr,从0 时刻到 k 时刻,其可能的模型切换轨 迹 为120,12{,,}kiiiktracekMmmm,其中kikm 表 示 K-1 到 K 时刻,模型切换到第ki 个,ki 可取1,2,,r ,即0,ktraceM总 共有kr 种 可能。再 令121,,,,kki iii为K+1 时刻经 由轨 迹0,ktraceM输入到第1ki 个模型滤波器的加 权 系数,则输入可以表 示 为 0,112112|,,,,|,,,ˆˆˆkktracekkkiMk ki ii ik ki iixx 可见 轨 迹0,ktraceM的复 杂 度 直 接 影 响 到算法计算量 和 存 储 量 。虽 然 全 轨 迹 的模式切换在理论上是最优的,但是其在k-1 到k 一个时间间隔的计算量(121,,,,kki iii的更新次数,滤波次数)就能达到kr 这个数量级,现实中根本无法实现。为了解决这一问题,目前的次优方法都是通过变换0,ktraceM模型切换轨迹的形式,在保证估计精度的情况下,减少算法计算量和存储量的。 具体的GPB1,GPB2,IMM 算法,是采用截断0,ktraceM的方式简化全轨迹的重初始化,下面给出他们与全轨迹方法重初始化的...